Chapter 9
Compressible Flow
Compressible Flow
Overview
Chapter 9 deals with compressible flow, which essentially is gas flows at high velocity (velocities comparable to the speed of sound) but more generally it is flows where the fluctuations in density are significant. In contrast to the flows studied in the previous chapters, density is not assumed to be constant when analyzing compressible flows and with large variations in pressure and temperature, the energy equation must be solved simultaneous with the momentum and continuity equations.
Mach Number Regimes
- Incompressible flow
- insignificant density changes
- Subsonic flow
- local and global Mach number less than unity
- Transonic flow
- subsonic flow with regions of supersonic flow (local Mach number can be higher than one)
- supersonic flow with regions of subsonic flow (local Mach number can be less than one)
- Supersonic flow
- local and global Mach number higher than one
- Hypersonic flow
- Mach number higher than 5.0
Roadmap
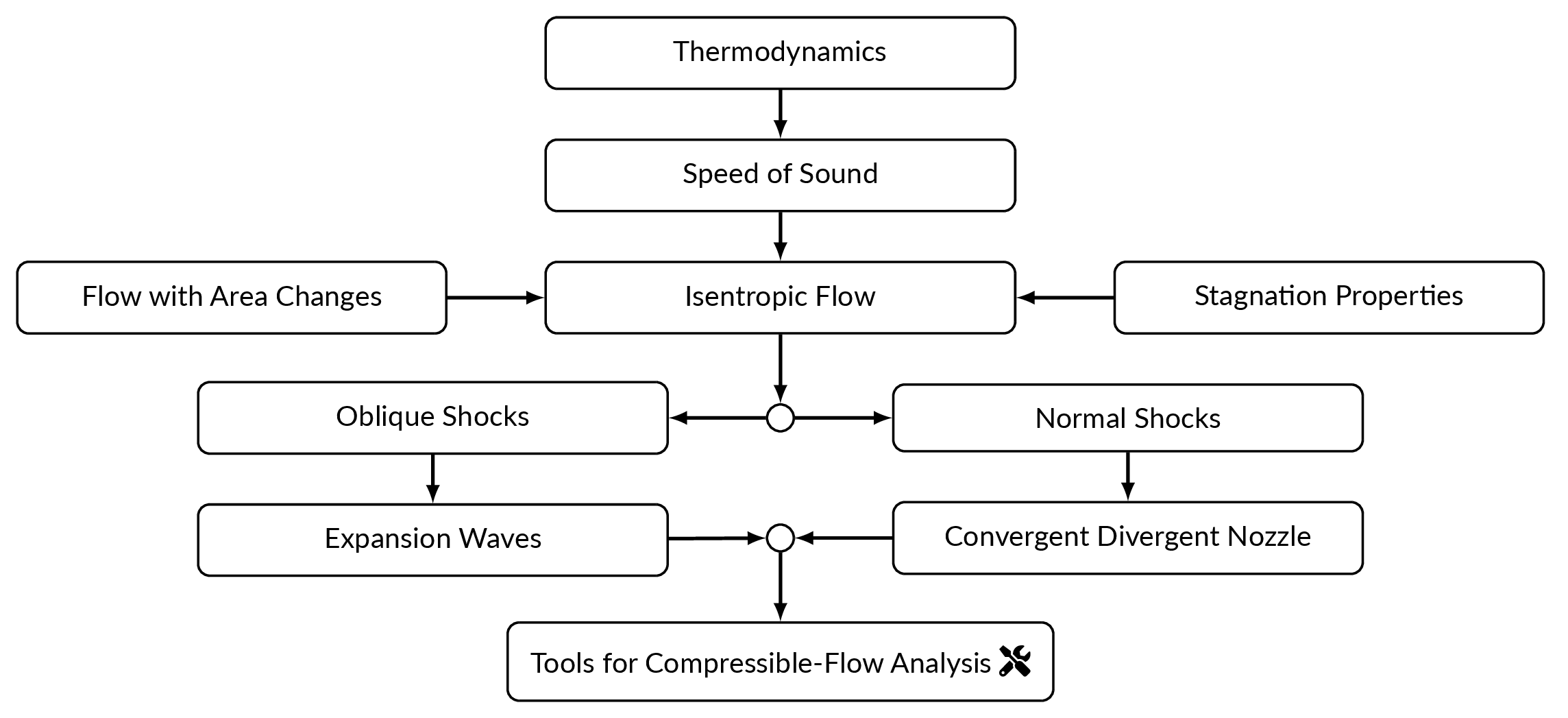
Thermodynamics Review
Gas flows at moderate temperatures will be considered, which means that the gas can be assumed to be calorically perfect. This means that the ideal gas law can be used and that specific heats are constant.
$$p=\rho RT$$$$R=C_p-C_v=const$$
$$\gamma=\frac{C_p}{C_v}=const$$
$$d\hat{u}=C_v dT$$
$$dh=C_p dT$$
Auxiliary relations
$$C_v=\frac{R}{\gamma-1},\ C_p=\frac{\gamma R}{\gamma-1}$$Isentropic Relations
First law of thermodynamics $$\delta q +\delta w=de$$For reversible processes: \(\delta w=-pd\upsilon\) (where \(\upsilon=p/\rho\))
$$h=e+\dfrac{p}{\rho}=e+p\upsilon\Rightarrow dh=de+pd\upsilon+\upsilon dp$$$$\delta q=dh-\upsilon dp$$
Second law of thermodynamics $$ds\ge\frac{\delta q}{T}$$
compute entropy change from the first and second law of thermodynamics.
$$Tds=dh-\frac{dp}{\rho}$$for perfect gases, \(dh=C_p dT\)
$$\int_1^2 ds=\int_1^2 C_p \frac{dT}{T}-R\int_1^2 \frac{dp}{p}$$for constant specific heats (calorically perfect)
$$s_2-s_1=C_p \ln \frac{T_2}{T_1}-R\ln\frac{p_2}{p_1}=C_v\ln \frac{T_2}{T_1}-R\ln\frac{\rho_2}{\rho_1}$$for isentropic flow \((s_2=s_1)\) we get
$$\frac{p_2}{p_1}=\left(\frac{T_2}{T_1}\right)^{\gamma/(\gamma-1)}=\left(\frac{\rho_2}{\rho_1}\right)^\gamma$$Speed of Sound
Speed of sound is a thermodynamic property related to the molecular activity of the fluid that describes the rate of propagation of a pressure pulse of infinitesimal strength through a fluid at rest. To derive an expression for the speed of sound, we will analyze a propagating wave using a control volume approach in the frame of reference following the propagating wave. The wave propagates in a fluid at rest, which means that in the frame of reference following the wave, the fluid velocity ahead of the wave will be the propagation velocity of the wave.
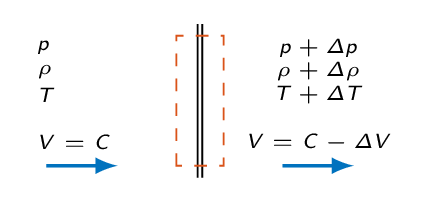
Mass balance over the control volume gives
$$\rho AC = (\rho + \Delta \rho) A (C-\Delta V)$$ $$\Delta V = C\frac{\Delta \rho}{\rho + \Delta \rho}$$Momentum balance
$$pA-(p+\Delta p)A=(\rho A C) (C-\Delta V -C) \Rightarrow \Delta p=\rho C \Delta V$$with \(\Delta V\) from the continuity equation we get
$$C^2=\frac{\Delta p}{\Delta \rho}\left(1+\frac{\Delta \rho}{\rho}\right)$$In the limit of infinitesimal strength \(\Delta \rho \rightarrow 0\) and thus
$$C^2=a^2=\frac{\partial p}{\partial \rho}$$There is no added heat and thus the process is adiabatic. For weak waves the process can also be assumed to be reversible
$$a^2=\left.\frac{\partial p}{\partial \rho}\right|_s$$The isentropic relation gives
$$p=\rho^\gamma\Rightarrow \frac{\partial p}{\partial \rho}=\gamma \rho^{\gamma-1}=\gamma\frac{p}{\rho}=\gamma RT$$and thus
$$a=\sqrt{\gamma R T}$$Stagnation Properties
Stagnation Enthalpy
The energy equation in one dimension
$$h_1+\frac{1}{2}V_1^2+gz_1=h_2+\frac{1}{2}V_2^2+gz_2-q+w_\nu$$Consider high-speed gas flow past an insulated wall
- No heat transfer
- Differences in potential energy are small
- Outside of the boundary layer, the flow is inviscid
The maximum enthalpy that the fluid would achieve if brought to rest adiabatically
For a calorically perfect gas \(h=C_pT\).
$$C_pT+\frac{1}{2}V^2=C_pT_o$$Where \(T_o\) is the stagnation temperature. Divide by \(C_pT\)
$$1+\frac{V^2}{2 C_p T}=\frac{T_o}{T}$$ $$C_p T=\frac{\gamma R}{\gamma-1}T=\frac{\gamma R T}{\gamma-1}=\frac{a^2}{\gamma-1}\Rightarrow \frac{T_o}{T}=1+\left(\frac{\gamma-1}{2}\right)M^2$$If the flow is assumed to be isentropic, the isentropic relations can be used to obtain expressions for \(p_o/p\) and \(\rho_o/\rho\).
- \(p_o\) and \(\rho_o\) - the pressure and density that the flow would achieve if brought to rest isentropically
- All stagnation properties are constants in an isentropic flow
- \(h_o\), \(T_o\), and \(a_o\) are constants in an adiabatic flow but not necessarily \(p_o\) and \(\rho_o\)
- \(p_o\) and \(\rho_o\) will vary throughout an adiabatic flow as the entropy changes due to friction or shocks
Critical Properties
Another useful set of reference variables is the critical properties (sonic conditions), which is the flow state that we would get if we eccelerated or decelerated the flow to sonic Mach number adiabatically.
$$\frac{T_o}{T}=1+\left(\frac{\gamma-1}{2}\right)M^2=\left\{M=1.0\right\}=1+\left(\frac{\gamma-1}{2}\right)=\left(\frac{2+\gamma-1}{2}\right)=\left(\frac{\gamma+1}{2}\right)$$$$\frac{T^\ast}{T_o}=\left(\frac{2}{\gamma+1}\right),\ \frac{a^\ast}{a_o}=\left(\frac{2}{\gamma+1}\right)^{1/2}$$
If the acceleration/deceleration process is also reversible, we can use the isentropic relations to calculate \(p^\ast\) and \(\rho^\ast\).
$$\frac{p^\ast}{p_o}=\left(\frac{2}{\gamma+1}\right)^{\gamma/(\gamma-1)},\ \frac{\rho^\ast}{\rho_o}=\left(\frac{2}{\gamma+1}\right)^{1/(\gamma-1)}$$
Isentropic Flow with Area Changes
Quasi-1D Flow
- Flow properties varies in one direction only \((x)\)
- The flow area is a smooth function \(A=A(x)\)
- Steady-state, inviscid and isentropic flow
The Area-Velocity Relation
The derivation of the area-velocity relation is done assuming isentropic flow.
Continuity:
$$\rho(x)V(x)A(x)=const \Rightarrow d(\rho VA)=0 \Rightarrow AVd\rho+\rho AdV+\rho VdA=0$$divide by \(\rho VA\) gives
$$\frac{d\rho}{\rho}+\frac{dV}{V}+\frac{dA}{A}=0$$Stagnation enthalpy:
$$h_o=h+\frac{1}{2}V^2=const\Rightarrow {\color{MatlabA}{dh}}+{\color{MatlabB}{VdV}}=0$$The first and second law of thermodynamics:
$$Tds=0=dh-\frac{dp}{\rho}\Rightarrow dh=\frac{dp}{\rho}$$and thus
$$\frac{dp}{\rho}+VdV=0$$From the definition of the speed of sound
$$dp=a^2 d\rho\Rightarrow a^2\frac{d\rho}{\rho}+VdV=0 \Rightarrow \frac{d\rho}{\rho} = -\frac{1}{a^2}VdV$$$$\frac{d\rho}{\rho}+\frac{dV}{V}+\frac{dA}{A}=\frac{dV}{V}-\frac{1}{a^2}VdV+\frac{dA}{A}=0$$
$$\frac{dV}{V}(M^2-1)=\frac{dA}{A}$$
This result is often referred to as the area-velocity relation. Interpretation of the relation is given in the figure below.
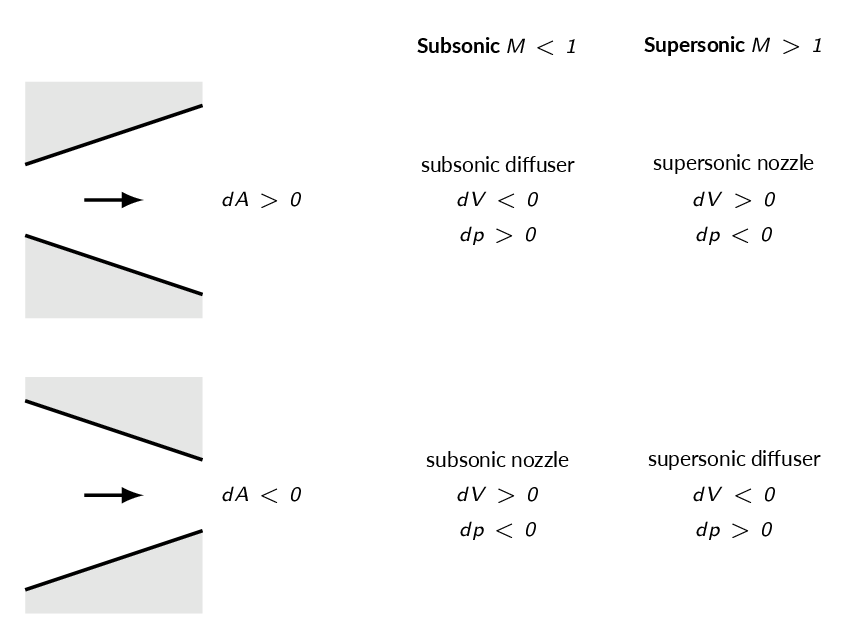
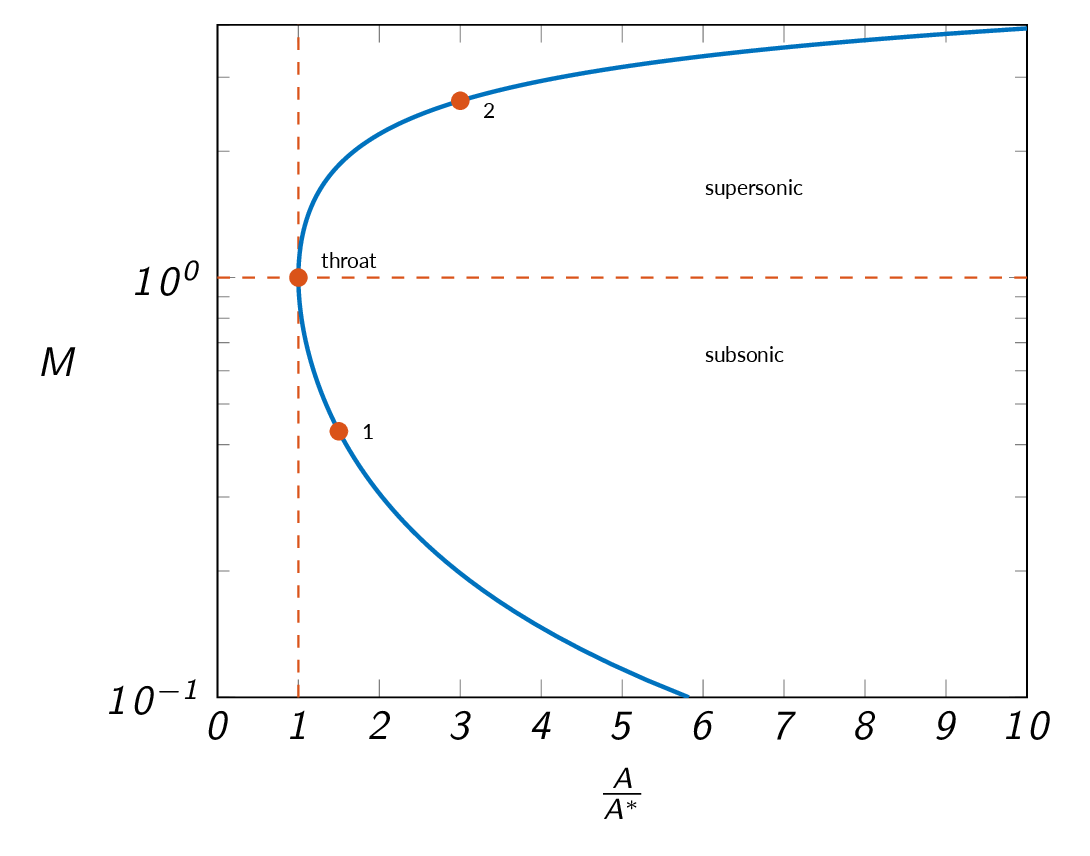
According to the area velocity relation, sonic flow \((M=1.0)\) occurs when \(dA\) is zero, i.e. either when the cross-section area is the smallest or the biggest. The figure below shows why sonic flow must occur at the smallest cross-section area.
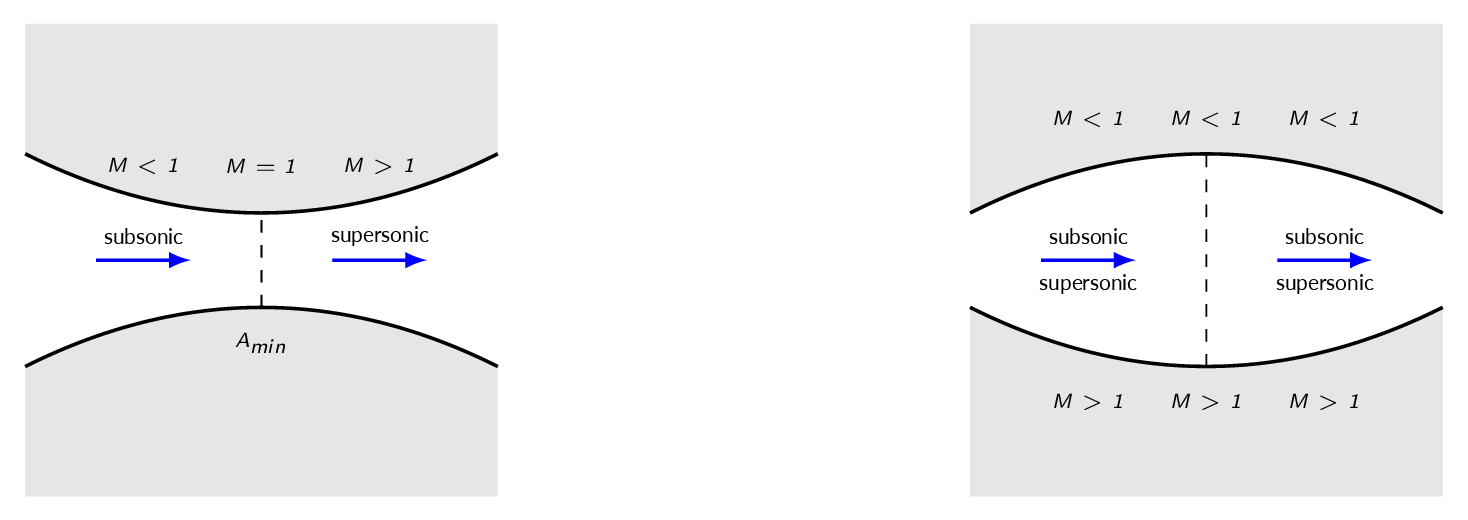
The Area-Mach Number Relation
The area-Mach-number relation is derived with the starting point in the continuity equation. The mass flow is constant and if evaluated at sonic conditions (starred flow quantities), we get
$$\rho AV=\rho^\ast A^\ast V^\ast \Rightarrow \frac{A}{A^\ast}=\frac{\rho^\ast}{\rho}\frac{V^\ast}{V}$$$$\frac{\rho^\ast}{\rho}=\frac{\rho^\ast}{\rho_o}\frac{\rho_o}{\rho}=\left[\frac{2}{\gamma+1}\left(1+\frac{\gamma-1}{2}M^2\right)\right]^{1/(\gamma-1)}$$
$$\frac{V^\ast}{V}=\frac{(\gamma RT^\ast)^{1/2}}{V}=\frac{(\gamma RT)^{1/2}}{V}\left(\frac{T^\ast}{T_o}\right)^{1/2}\left(\frac{T_o}{T}\right)^{1/2}=\frac{1}{M}\left[\frac{2}{\gamma+1}\left(1+\frac{\gamma-1}{2}M^2\right)\right]^{1/2}$$
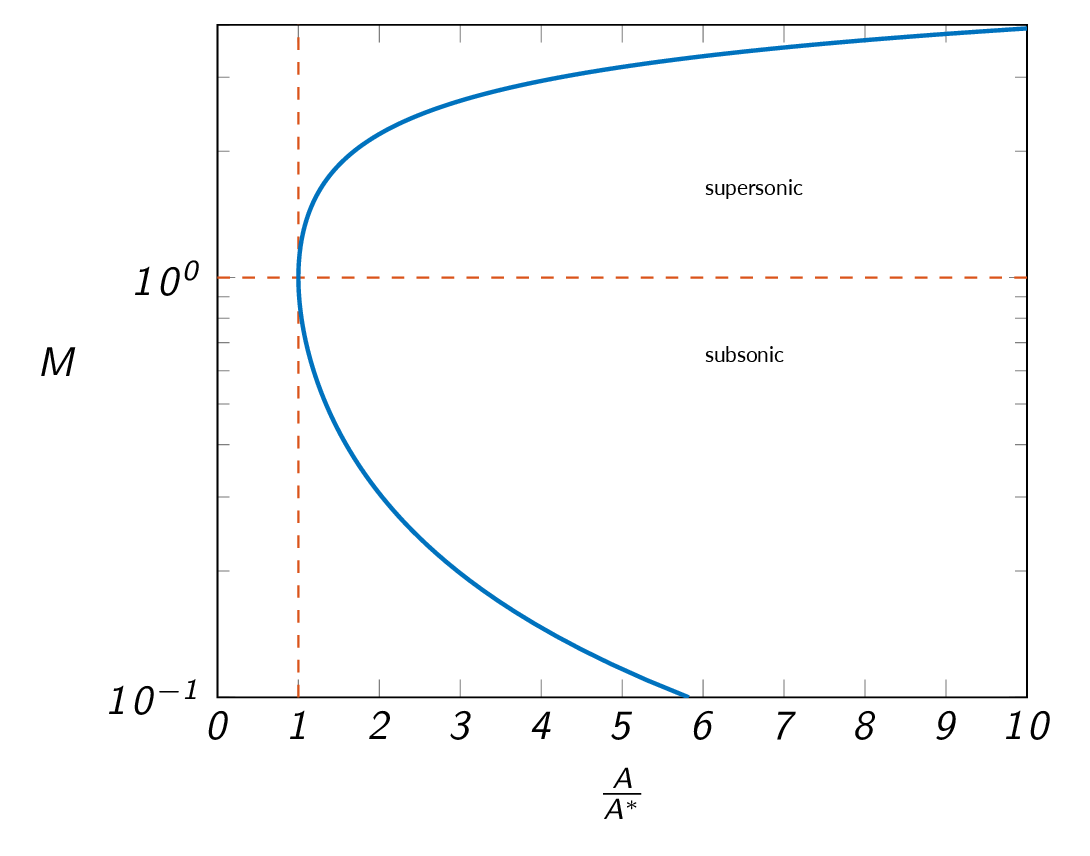
Combined, these relations results in the area-Mach-number relation.
$$\left(\frac{A}{A^\ast}\right)^2=\frac{1}{M^2}\left[\frac{2+(\gamma-1)M^2}{\gamma+1}\right]^{(\gamma+1)/(\gamma-1)}$$The area-Mach-number relation is plotted in the figure below. It should be noted that since the relation is quadratic, it has two solutions for each area ratio, one subsonic and one supersonic (except for at sonic conditions).
Let's see what the Mach-number distribution in a convergent divergent nozzle, as the one depicted below, looks like for a subsonic case and for a case where sonic velocity is reached at the throat of the nozzle and the flow remains supersonic throughout the nozzle.
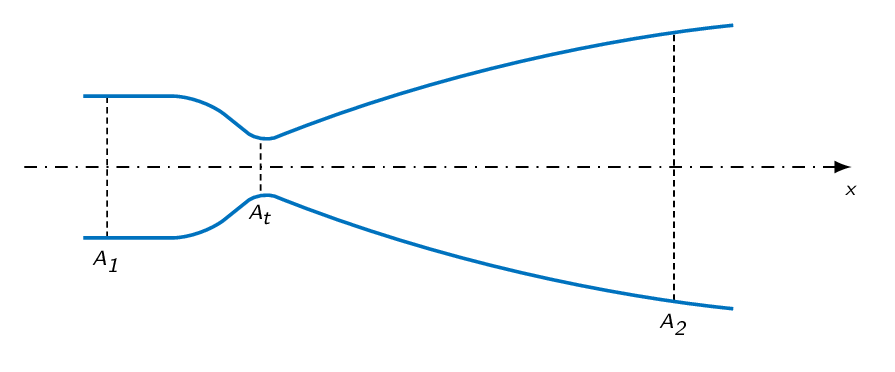
Subsonic flow in the entire nozzle:
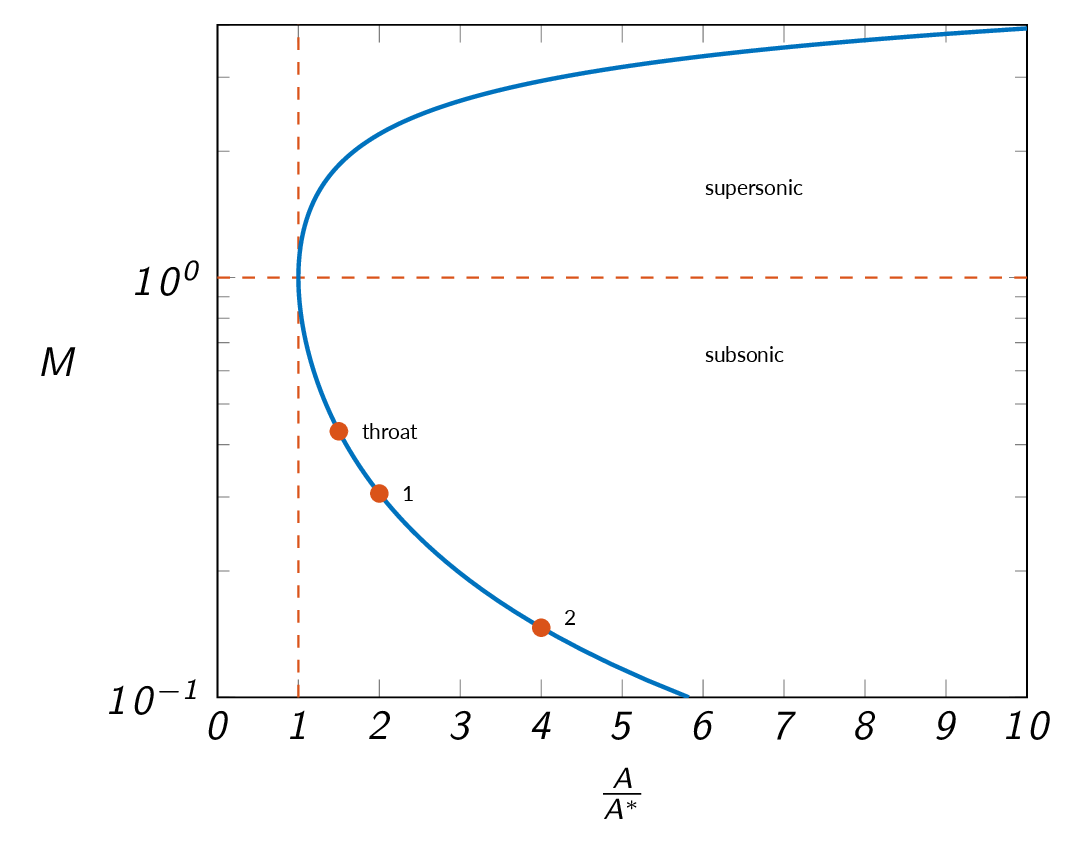
Subsonic flow in the convergent part of the nozzle, sonic flow at the throat, and supersonic flow in the divergent part of the nozzle:
Choked Flow
Continuity
$$\rho VA=\rho^\ast A^\ast V^\ast \Rightarrow \frac{A^\ast}{A}=\frac{\rho V}{\rho^\ast V^\ast}$$From the area-Mach-number relation
$$ \frac{A^\ast}{A}= \left\{ \begin{array}{lll} <1 & \text{if } & M<1\\ 1 & \text{if } & M=1\\ <1 & \text{if } & M>1 \end{array} \right. $$The maximum possible mass flow through a duct is achieved when its throat reaches sonic conditions.
$$\dot{m}_{max}=\rho^\ast A^\ast V^\ast$$with
$$\frac{\rho^\ast}{\rho_o}=\left(\frac{2}{\gamma+1}\right)^{1/(\gamma-1)},\ V^\ast=\sqrt{\gamma RT^\ast},\ \text{and}\ \frac{T^\ast}{T_o}=\frac{2}{\gamma+1}$$The choked mass flow is obtained as
$$\dot{m}_{max}=\frac{A^\ast p_o}{\sqrt{T_o}}\sqrt{\frac{\gamma}{R}\left(\frac{2}{\gamma+1}\right)^{\frac{(\gamma+1)}{(\gamma-1)}}}$$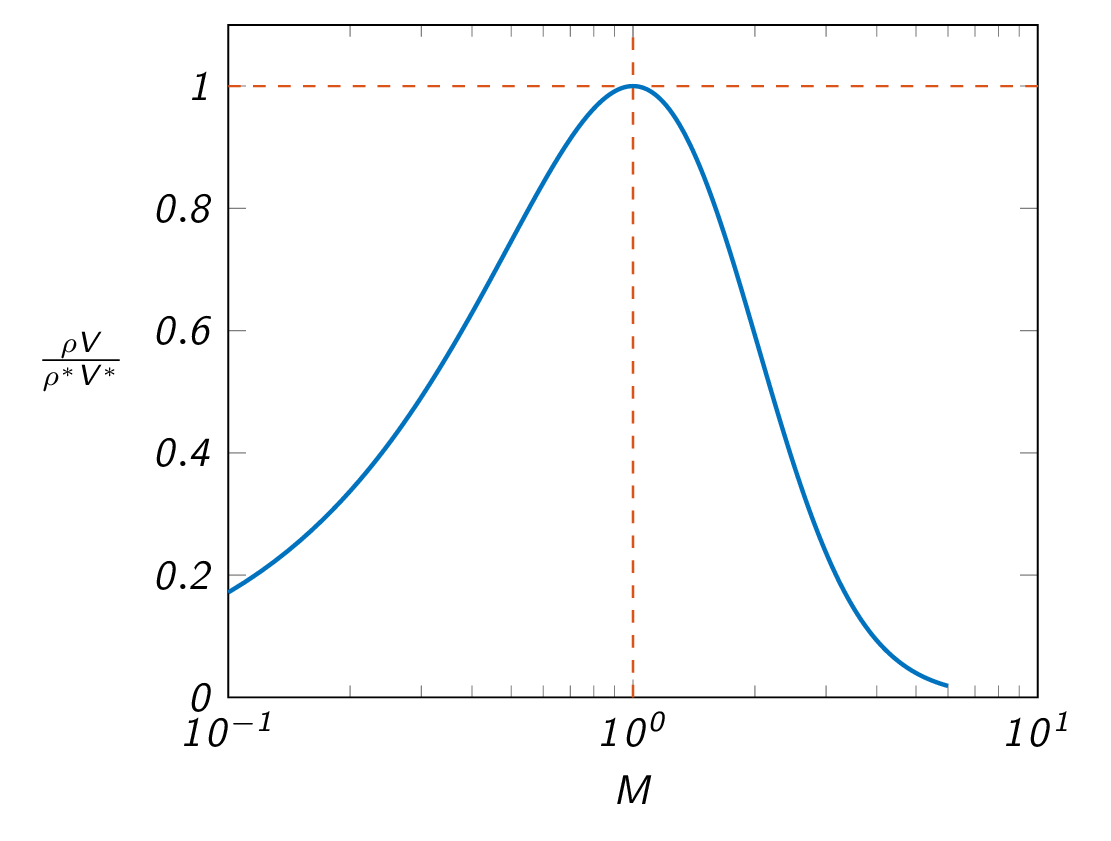
Normal Shocks
Shock waves are nearly discontinuous changes in a supersonic flow
Reasons for the appearance of shocks in a flow can be for example:
- higher downstream pressure
- sudden changes in flow direction
- blockage by a downstream body
- an explosion
We will use a control volume approach to derive the normal-shock relations. Steady-state, adiabatic, inviscid flow in one dimension will be assumed.
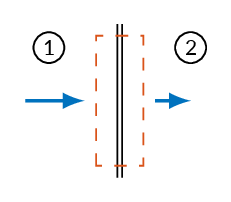
Continuity:
$$\rho_1 u_1=\rho_2 u_2$$Momentum:
$$p_1-p_2=\rho_2 u_2^2-\rho_1 u_1^2$$Energy:
$$h_1+\frac{1}{2}u_1^2=h_2+\frac{1}{2}u_2^2=h_o$$Combining the three governing equations above, a relation called the Rankine-Hugoniot equation can be derived. The Rankine-Hugoniot equation describes the relation of thermodynamic properties over a normal shock. The fact that the relation only includes thermodynamic properties means that it can be used with the same results even if the frame of reference is changed, which is helpful for moving shocks.
$$h_2-h_1=\frac{1}{2}(p_2-p_1)\left(\frac{1}{\rho_2}+\frac{1}{\rho_1}\right)$$From the laws of thermodynamics we get
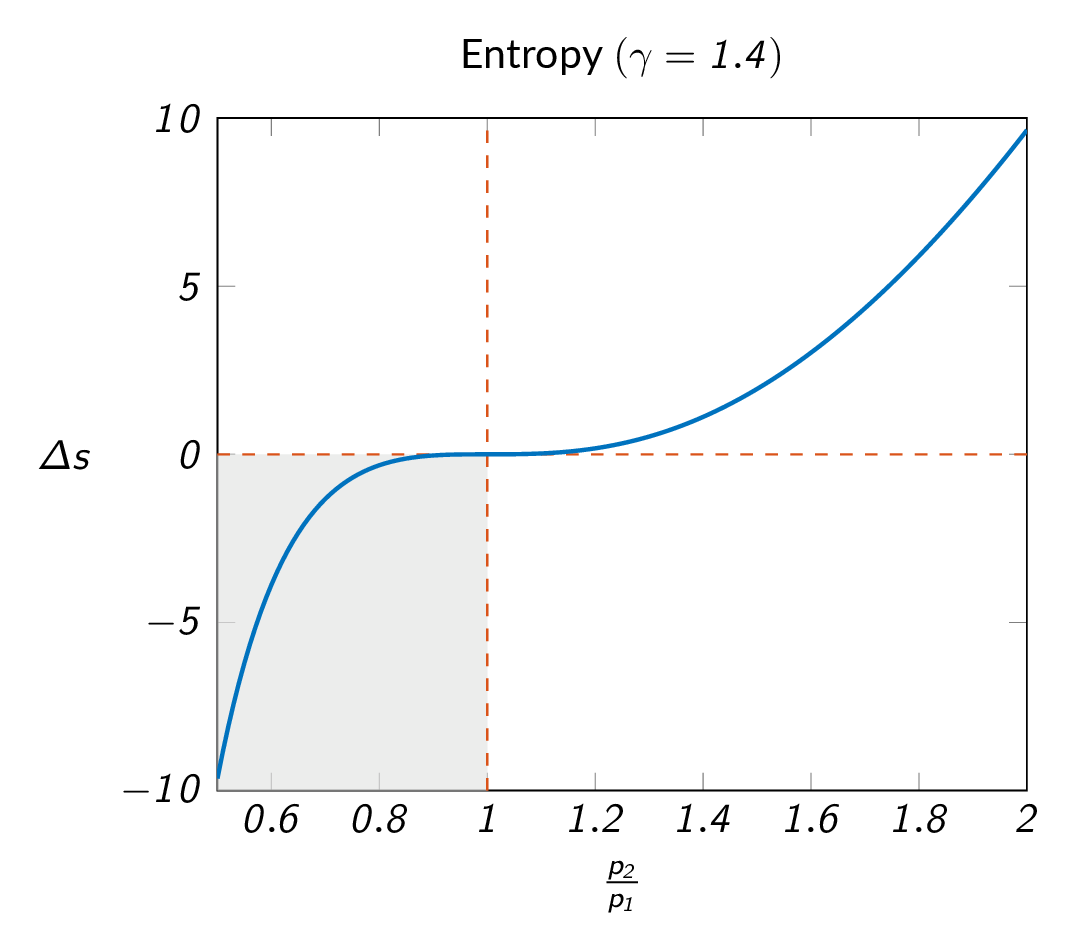
$$s_2-s_1=C_p\ln\frac{T_2}{T_1}-R\ln\frac{p_2}{p_1}$$which may be rewritten as follows
$$s_2-s_1=C_v\ln\left[\frac{p_2}{p_1}\left(\frac{\rho_1}{\rho_2}\right)^\gamma\right]$$With the density ratio from the Rankine-Hugoniot relation, one can plot the entropy change as a function of pressure ratio. As can be seen from the figure below, a pressure ratio less than one over the shock would imply a reduction in entropy, which is not physical. Therefore, one can make the conclusion that the pressure ratio over the shock must be one or greater.
Normal-Shock Relations
A relation describing the change in pressure over a normal shocks is obtained by rewriting the momentum equation and using the continuity and energy equations.
$$p_2-p_1=\rho_1 u_1^2-\rho_2 u_2^2=\{\rho_1 u_1=\rho_2 u_2\}=\rho_1 u_1(u_1-u_2)=\rho_1 u_1^2\left(1-\frac{u_2}{u_1}\right)$$divide by \(p_1\)
$$\frac{p_2}{p_1}=1+\frac{\rho_1 u_1^2}{p_1}\left(1-\frac{u_2}{u_1}\right)$$$$u_1^2=M_1^2 a_1^2=M_1^2\gamma RT_1=\gamma M_1^2\frac{p_1}{\rho_1}\Rightarrow\frac{p_2}{p_1}=1+\gamma M_1^2\left(1-\frac{u_2}{u_1}\right)$$
From the energy equation, the following relation for \(u_2/u_1\) can be obtained
$$\frac{u_2}{u_1}=\frac{2+(\gamma-1)M_1^2}{(\gamma+1)M_1^2}$$Inserted in the relation above, this gives
$$\frac{p_2}{p_1}=1+\frac{2\gamma}{\gamma+1}\left(M_1^2-1\right)$$The figure below shows how the pressure ratio over the shock varies with upstream Mach number. From before we know that the pressure ratio over the shock must be 1.0 or greater and thus the Mach number before the shock must be 1.0 or greater. To get a discontinuity in flow properties, the upstream Mach number must be greater than 1.0. If the upstream Mach number is equal to 1.0, a Mach wave may be formed, which is not the same as a normal shock since a Mach wave will not lead to any significant changes of flow properties.
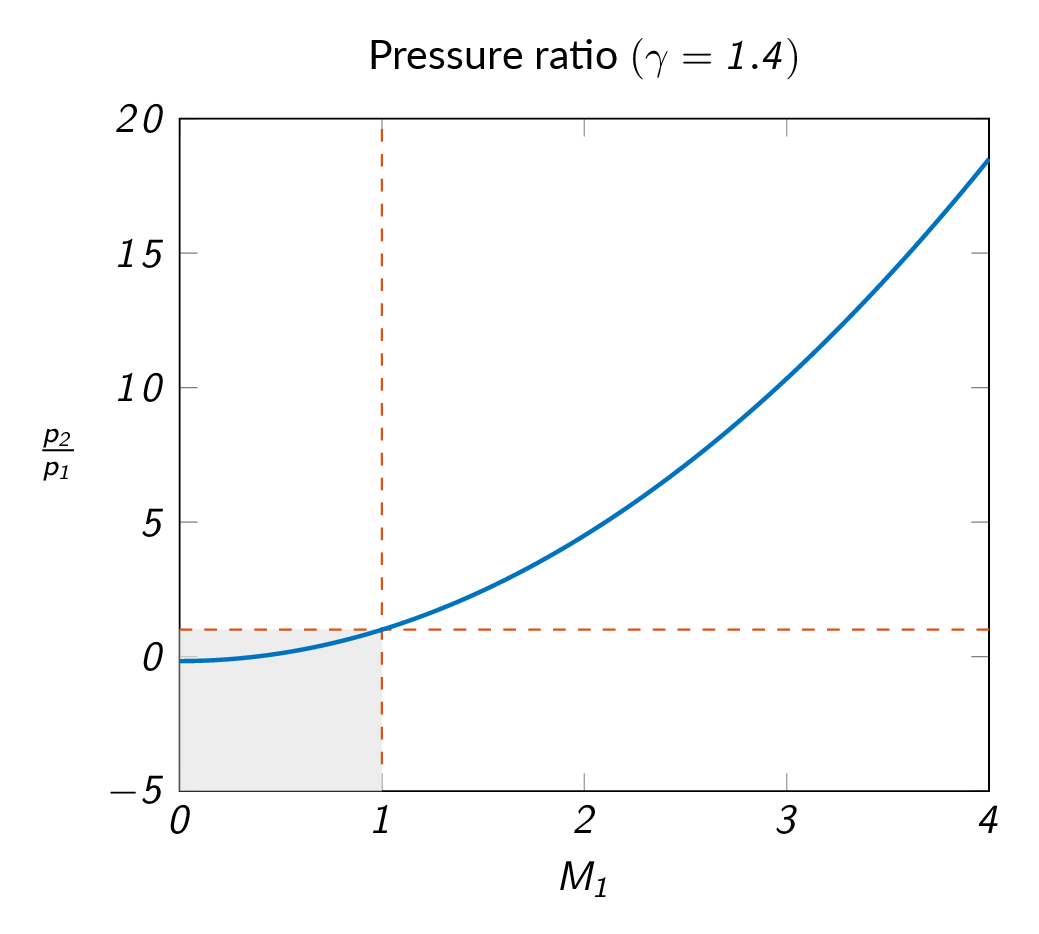
Going back to the momentum equation
$$p_1+\rho_1 u_1^2=p_2+\rho_2 u_2^2$$$$M=\frac{u}{a}\Rightarrow p_1+\rho_1 M_1^2a_1^2=p_2+\rho_2 M_2^2 a_2^2$$
$$a=\sqrt{\gamma RT}=\sqrt{\frac{\gamma p}{\rho}}\Rightarrow p_1+\rho_1 M_1^2 \frac{\gamma p_1}{\rho_1}=p_2+\rho_2 M_2^2 \frac{\gamma p_2}{\rho_2}$$
$$p_1\left(1+ \gamma M_1^2\right)=p_2\left(1+ \gamma M_2^2\right)$$
$$\frac{p_2}{p_1}=\frac{1+ \gamma M_1^2}{1+ \gamma M_2^2}$$
Now we have two relations for the pressure ratio over the shock and by combining these relation we can derive a relation for the change of Mach number over the shock. The Mach number downstream of the shock is given by
$$M_2^2=\frac{(\gamma-1)M_1^2+2}{2\gamma M_1^2 -(\gamma-1)}$$The figure below shows how the downstream Mach number varies with upstream Mach number. Downstream of a normal shock, the Mach number will always be less than 1.0, i.e. the flow will be subsonic.
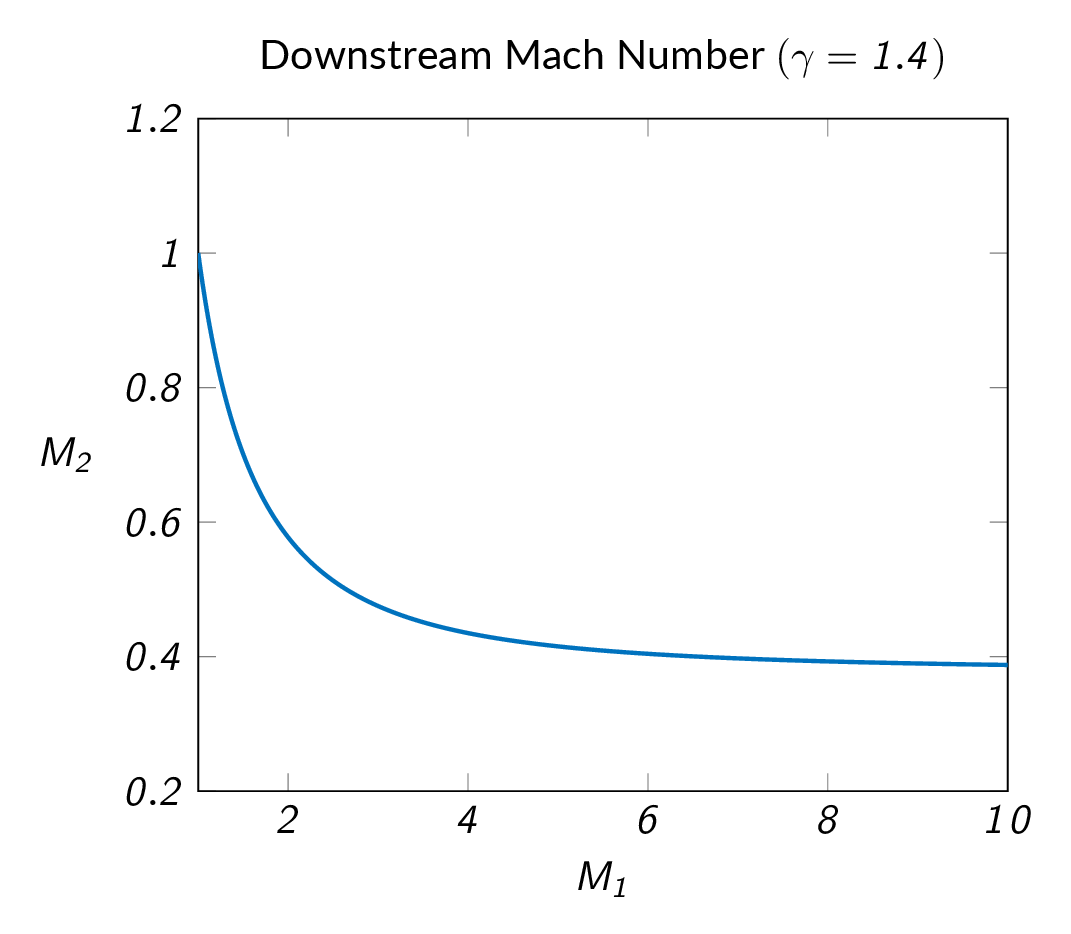
From the normal-shock relations derived above, relations for other flow properties can be derived. The figure below shows some of these relations graphically.
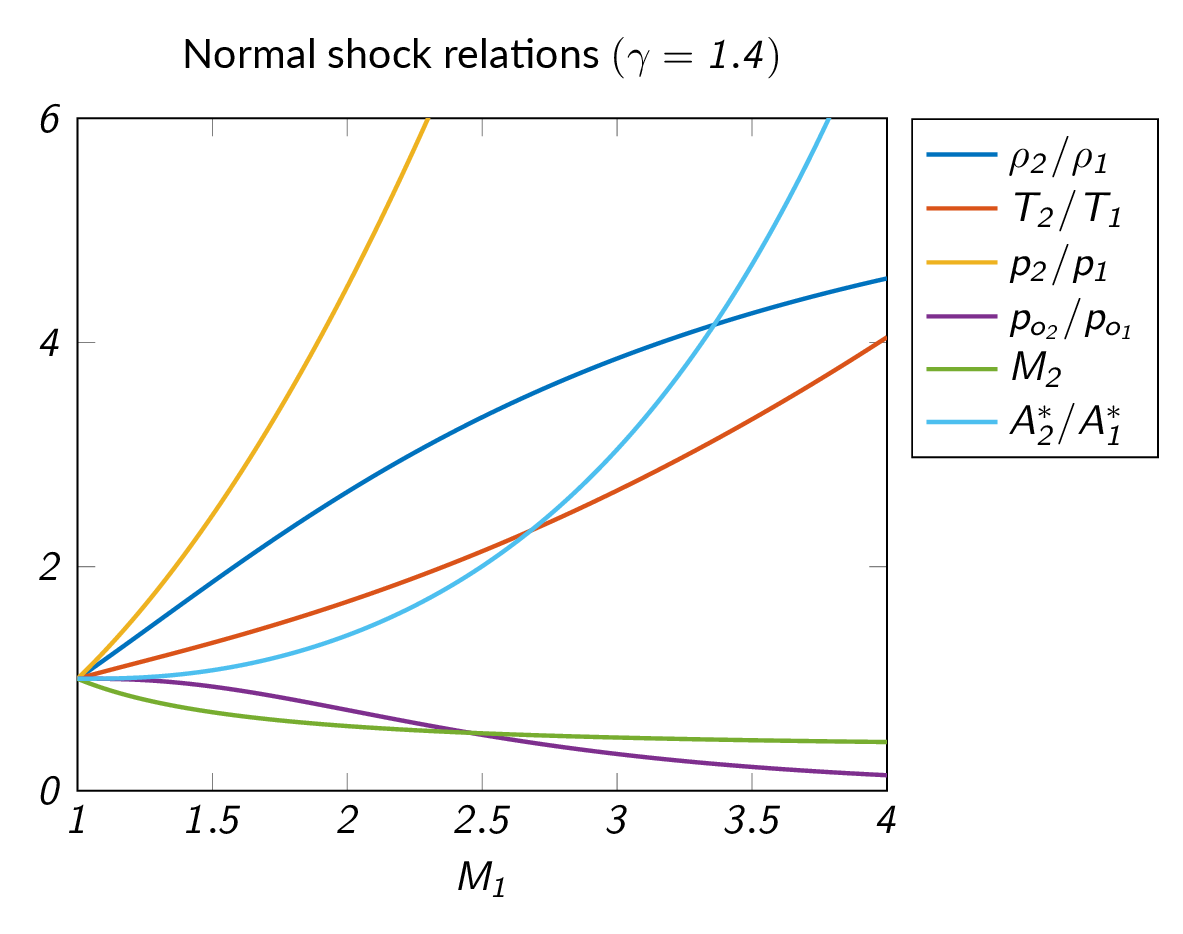
Normal-Shock Relations - Summary
- Supersonic flow upstream of normal shock
- Subsonic flow downstream of normal shock
- Entropy increases over the shock and consequently total pressure decreases
- Sonic throat area increases
- Very weak shock waves are nearly isentropic
The Convergent-Diveregent Nozzle
The series of figures below shows how the Mach number and pressure distribution varies with nozzle-pressure ratio, i.e. the inlet total pressure divided by the exit back pressure. The nozzle pressure ratio is assumed to be increased by lowering the back pressure. In the first of the figures, the flow is subsonic through the nozzle. The Mach number is increased in the convergent part of the nozzle but does not reach sonic conditions at the throat and thus the flow in the divergent part of the nozzle will be defined by the subsonic branch of the area-Mach number relation. The flow is isentropic (inviscid flow without addition of heat and shocks) which means that both \(p_o\) and \(T_o\) are constant through the nozzle. The mass flow is below the choked mass flow.
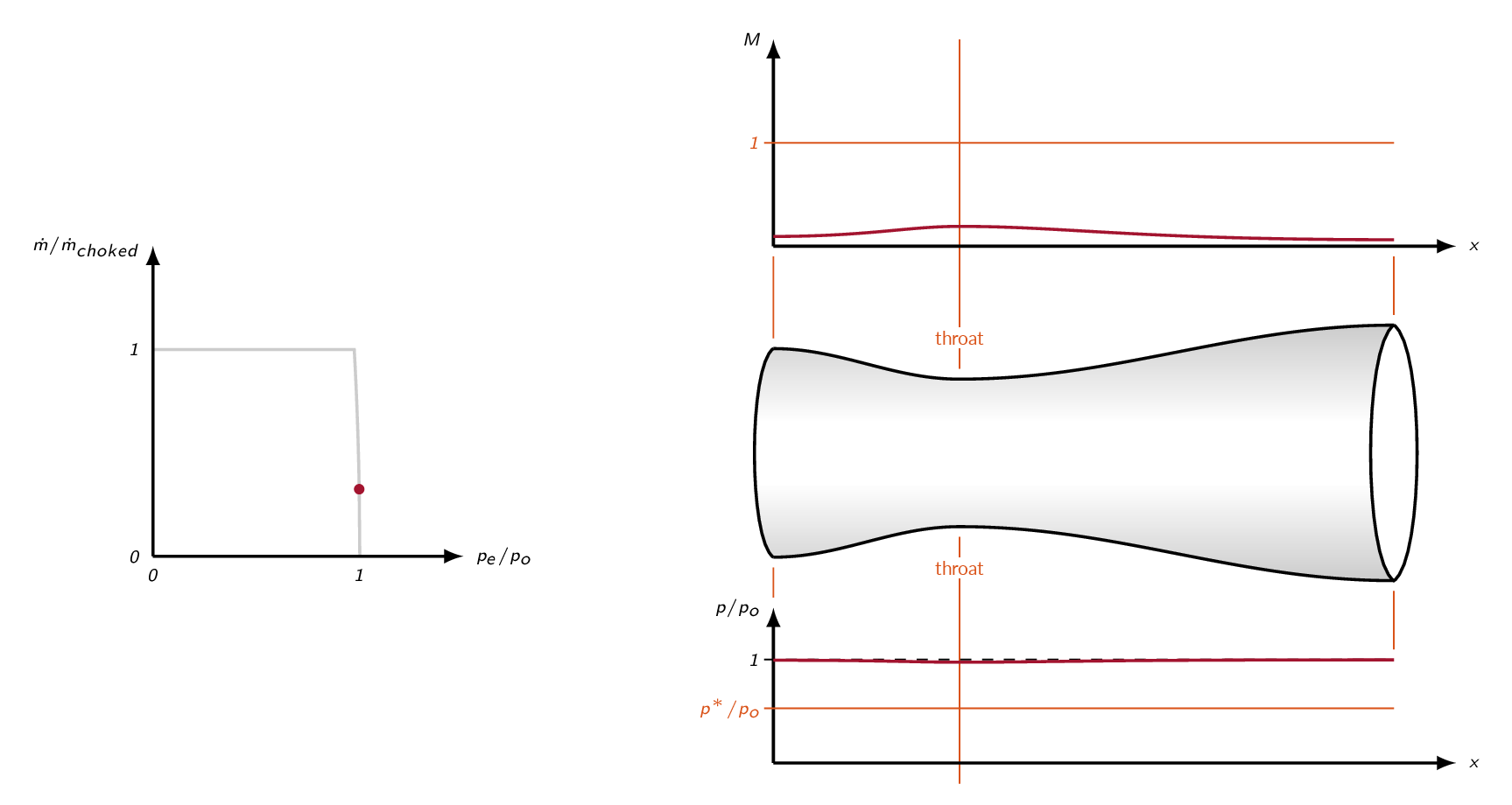
In the next figure, the pressure ratio over the nozzle has been increased such that the Mach number at the throat is 1.0 (sonic flow). Downstream of the throat, the flow will still be subsonic though. In order to get supersonic flow downstream of the throat the nozzle pressure ratio must be increased. With sonic flow at the throat, the choked mass flow is reached.

Increasing the pressure ratio over the nozzle over the choked flow pressure ratio, the flow in the divergent part of the nozzle will initially be supersonic following the supersonic branch of the area-Mach-number relation. In order to match the downstream pressure at the exit, a shock will form somewhere inside the nozzle. The axial location where the shock appears depends on the back pressure. Downstream of the shock, the flow will be subsonic and thus following the subsonic branch of the area-Mach-number relation. It should be noted, however, that the normal shock leads to a change of the sonic area \((A^\ast)\). Since the nozzle pressure ratio is increased by lowering the back pressure the mass flow is fixed to the choked mass flow (if one instead increase the pressure ratio by increasing the inlet total pressure, the mass flow will be increased). The shock leads to an increase of entropy and thus the stagnation pressure is not constant. The stagnation temperature is still constant since there is no heat added to the flow.

Increasing the nozzle pressure ratio further moves the normal shock downstream in the divergent part of the nozzle and eventually the normal shock will be placed at the nozzle exit plane (normal shock at exit condition).
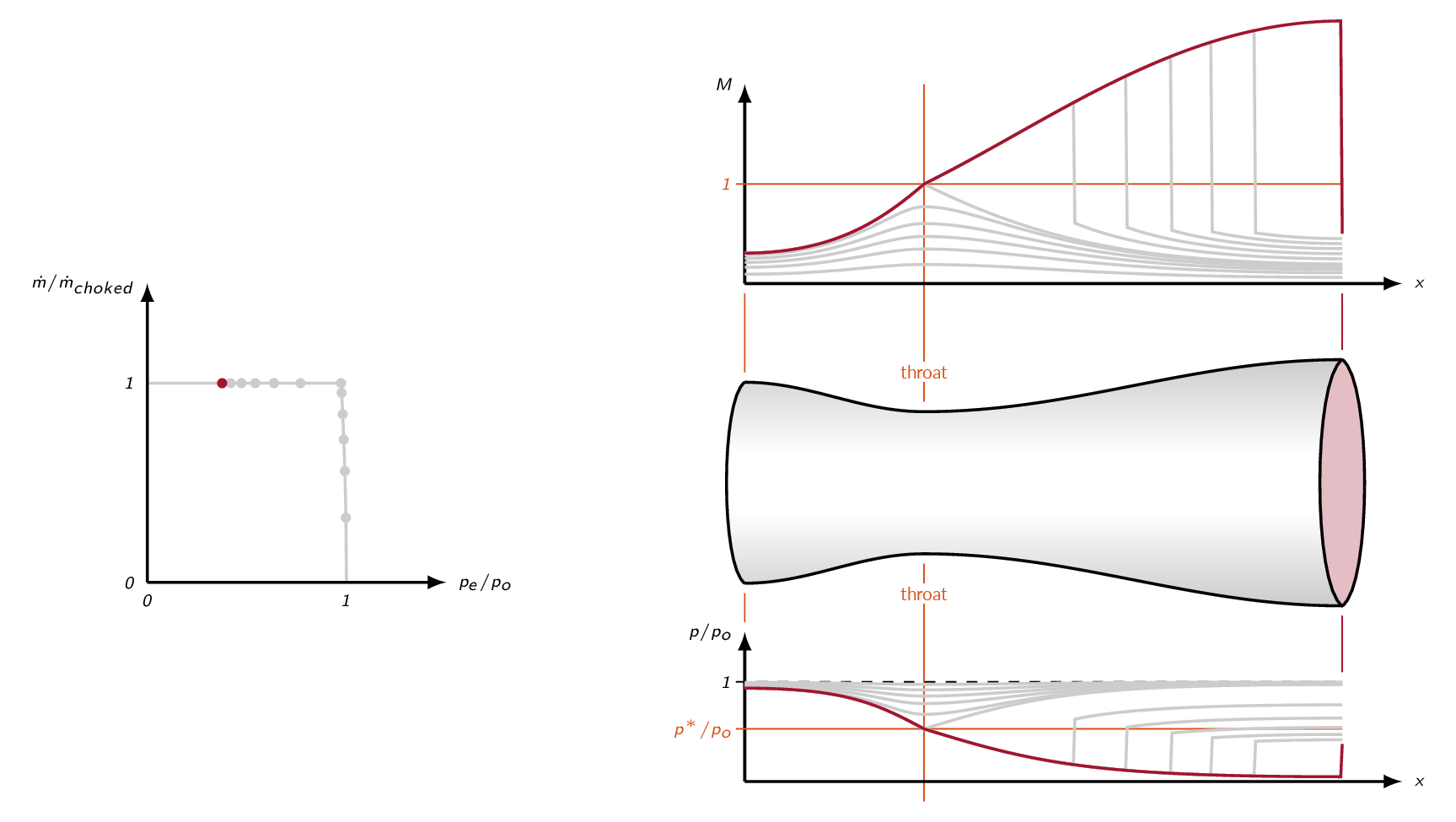
For pressure ratios higher than the normal-shock-at-exit pressure ratio, the flow through the divergent part of the nozzle will be supersonic without shocks.
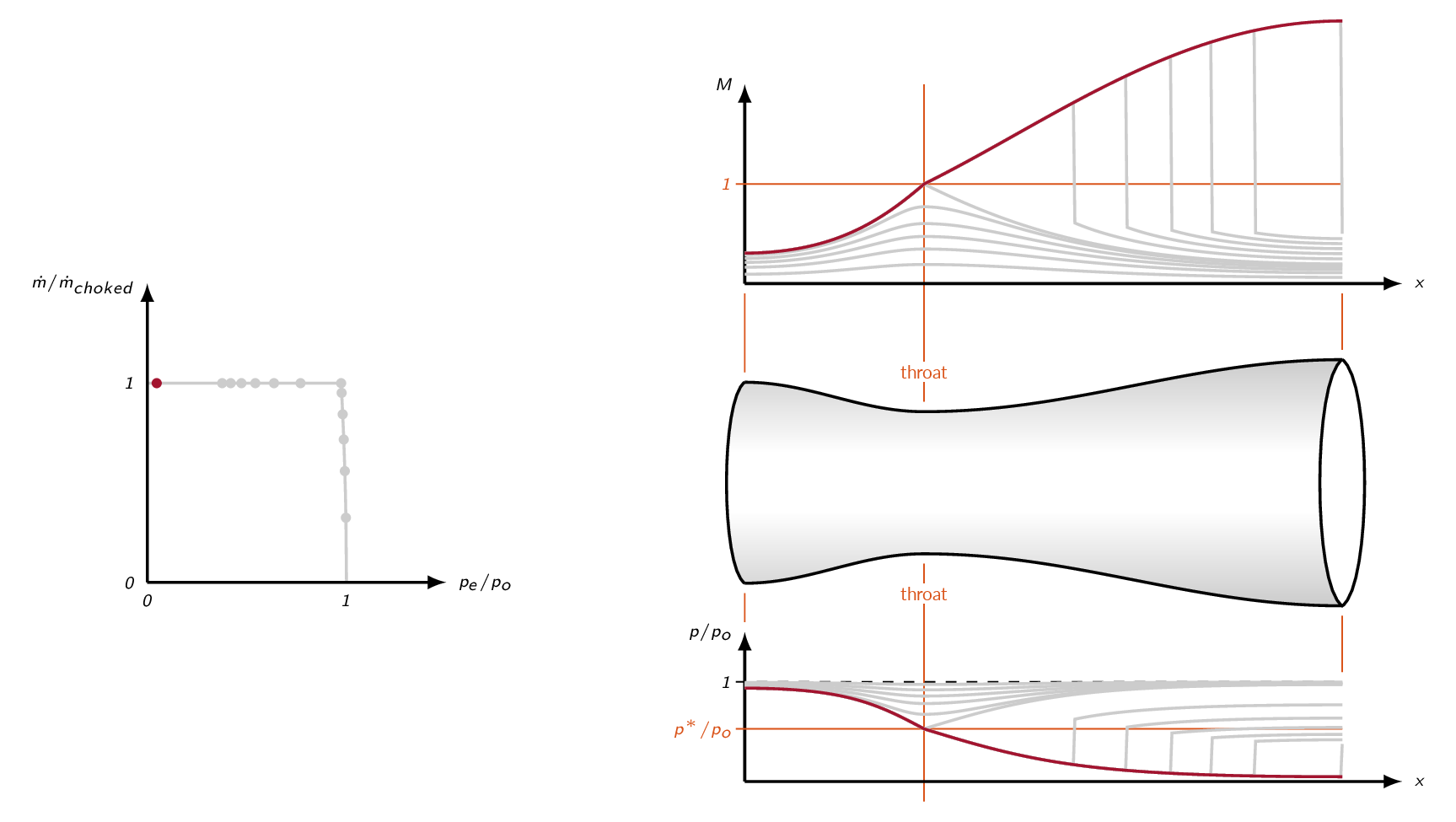
The figure below illustrates the flow downstream of the nozzle exit for nozzle pressure ratios higher than the normal-shock-at-exit pressure ratio. An increased pressure ratio leads to the formation of oblique shocks downstream of the nozzle exit (over-expanded flow). For one specific nozzle pressure ratio the supersonic flow will be perfectly matched at the exit and the downstream flow will be free of shocks and expansion regions (supercritical condition). For pressure ratios higher than the supercritical condition, the nozzle will be under-expanded and expansion regions will be formed downstream of the nozzle exit.
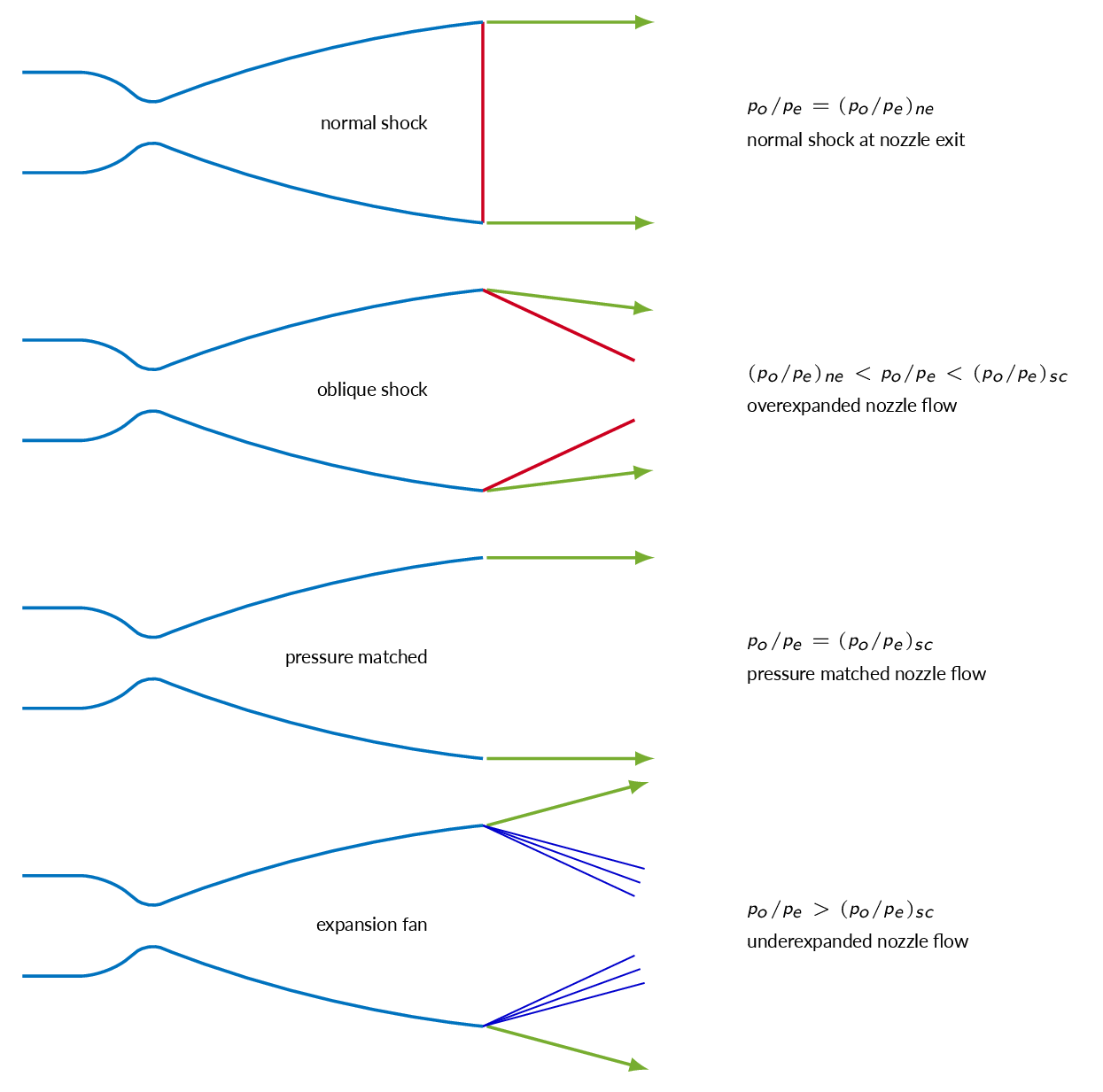
Oblique Shocks
The figures below shows the sound field generated as a sound transmitter emits sound as it moves with different velocities. In the top figure the sound transmitter is stationary, which leads to a sound pattern of circles centered at the location of the transmitter. The sound waves moves with the speed of sound. In the lower left figure the transmitter moves with a subsonic velocity to the left. This means that the sound pattern will be effected such that the frequency will be higher ahead of the transmitter and lower behind the transmitter (Doppler shift). In the lower mid figure, the transmitter moves at sonic speed, which means that the transmitter will always be located at the wave front (the acoustic waves moves with the same velocity as the transmitter). Finally, in the lower right figure, the transmitter moves with a supersonic velocity and thus it will always be ahead of the sound waves.
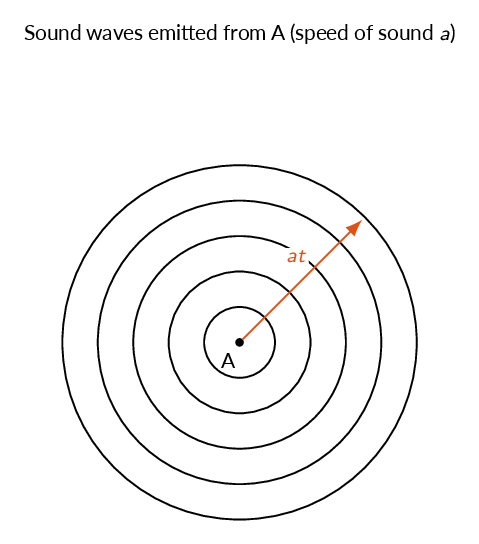
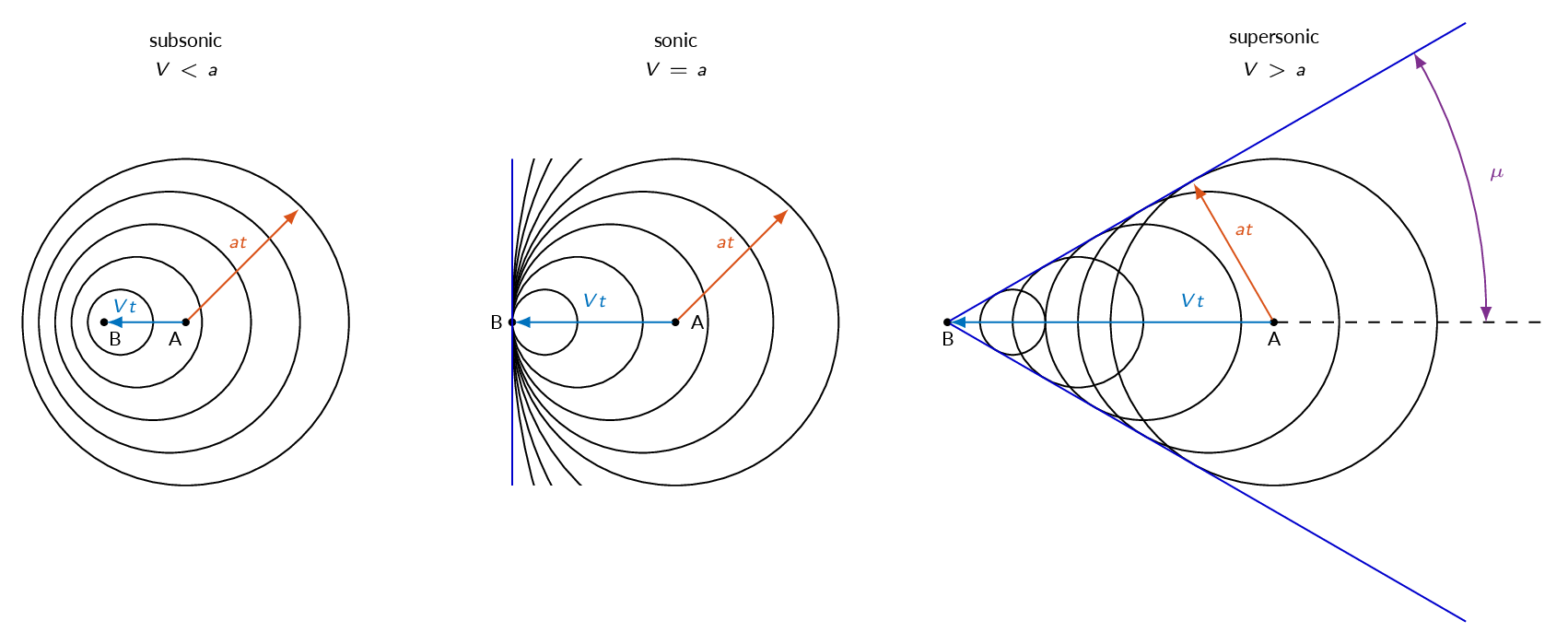
The sound waves generated by the supersonic transmitter forms a Mach wave with the angle \(\mu\).
$$\sin \mu=\dfrac{at}{Vt}=\dfrac{a}{V}=\dfrac{1}{M}$$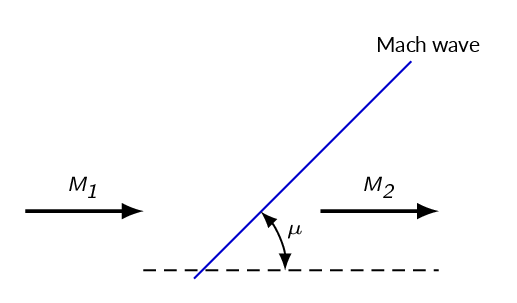
A Mach wave is an infinitely weak oblique shock. A single Mach wave is isentropic and will not lead to any significant changes in flow properties.
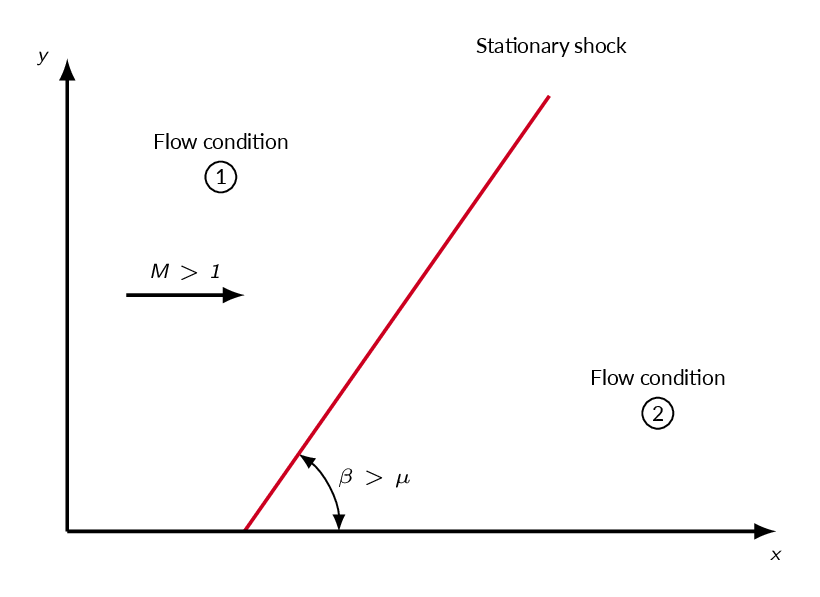
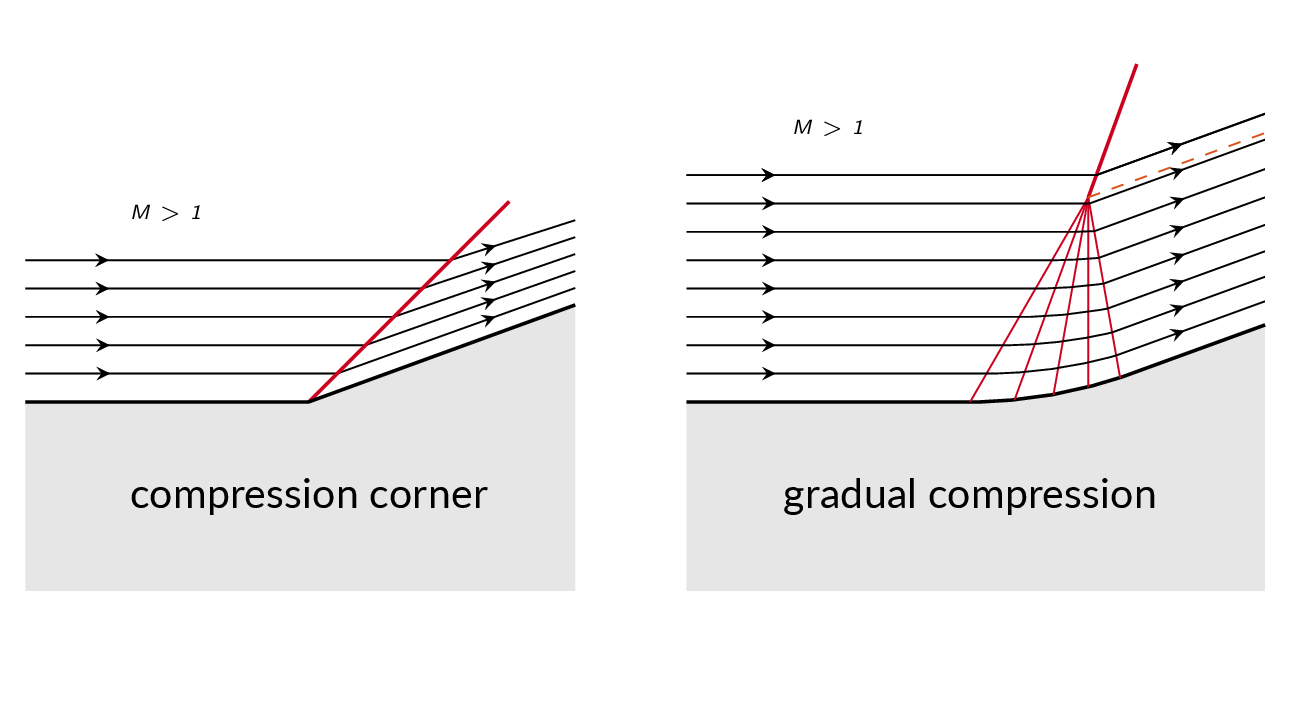
An oblique shock is, unlike a Mach wave, not isentropic and leads to significant changes in flow properties. The shock angle \(\beta\) will always be greater than the Mach angle \(\mu\) for a specific Mach number. An oblique shock is formed in the flow when there is a need for change of flow direction. Two examples are shown below. The left figure shows supersonic flow over a wall where there is a sudden change in direction. An oblique shock will be formed at the corner such that the flow direction after the shock follows the wall. The example in the right figure shows a continuous change in flow direction, which will form a compression region (a large number of Mach waves that successively bends the flow such that it follows the wall). The angle of consecutive Mach waves grows downstream since the mach number is continuously decreased and the Mach wave angle is a function of the Mach number. This means that the compression Mach waves will eventually meet somewhere away from the wall and coalesce into an oblique shock.
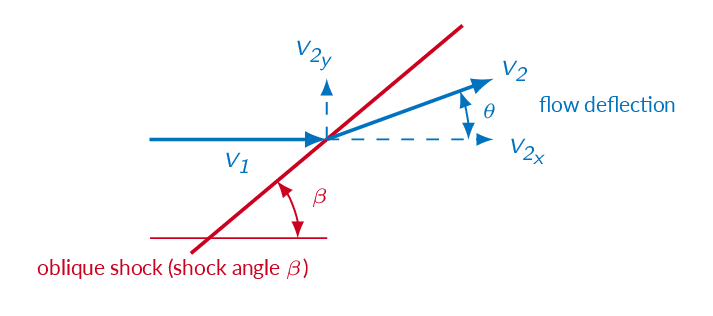
The figure below shows the important angles for an oblique shock. \(\beta\) is the shock angle and \(\theta\) is the flow deflection angle .
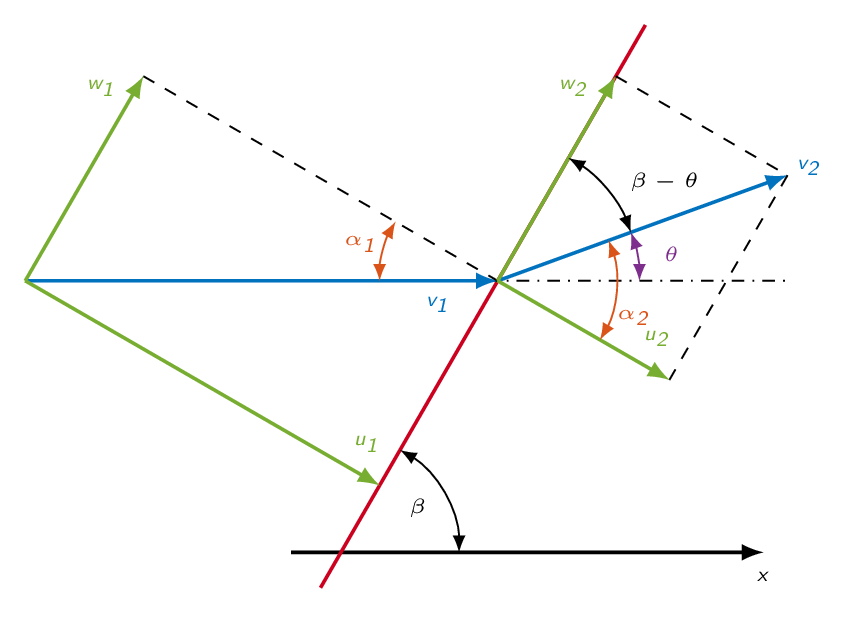
In order to analyze the oblique shock, a control volume is set up such that the inlet and the outlet are aligned with the shock and have the same area \(A\). The rest of the control volume surfaces are aligned with the flow upstream and downstream of the shock, respectively.

Conservation of mass
$$-\rho_1 u_1 A+\rho_2 u_2 A=0 \Rightarrow \rho_1 u_1=\rho_2 u_2$$Conservation of momentum (shock-normal direction)
$$-(\rho_1 u_1^2 +p_1)A+(\rho_2 u_2^2 +p_2)A=0 \Rightarrow \rho_1 u_1^2 +p_1=\rho_2 u_2^2 +p_2$$Conservation of momentum (shock-tangential direction)
$$-\rho_1 u_1 w_1 A+ \rho_2 u_2 w_2 A=0 \Rightarrow w_1=w_2$$Conservation of energy
$$-\rho_1 u_1 [ h_1+\frac{1}{2}(u_1^2+w_1^2)] A+ \rho_2 u_2 [ h_2+\frac{1}{2}(u_2^2+w_2^2)] A=0 \Rightarrow h_1+\frac{1}{2}u_1^2=h_2+\frac{1}{2}u_2^2$$The result is that in the shock-normal direction we can use the normal-shock relations if the shock-normal Mach number is used.
$$u_1=v_1 \sin(\beta)\Rightarrow M_{n_1}=\dfrac{u_1}{a_1}=\dfrac{v_1}{a_1}\sin(\beta)=M_1\sin(\beta)$$ $$u_2=v_2 \sin(\beta-\theta)\Rightarrow M_{n_2}=\dfrac{u_2}{a_2}=\dfrac{v_2}{a_2}\sin\beta=M_2\sin(\beta-\theta)$$Note! relations describing the change in stagnation properties over a normal shock cannot be used for an oblique shock since the stagnation properties are defined using the flow Mach number (not the shock-normal Mach number), which includes the shock-tangential velocity component.
Shock Polar
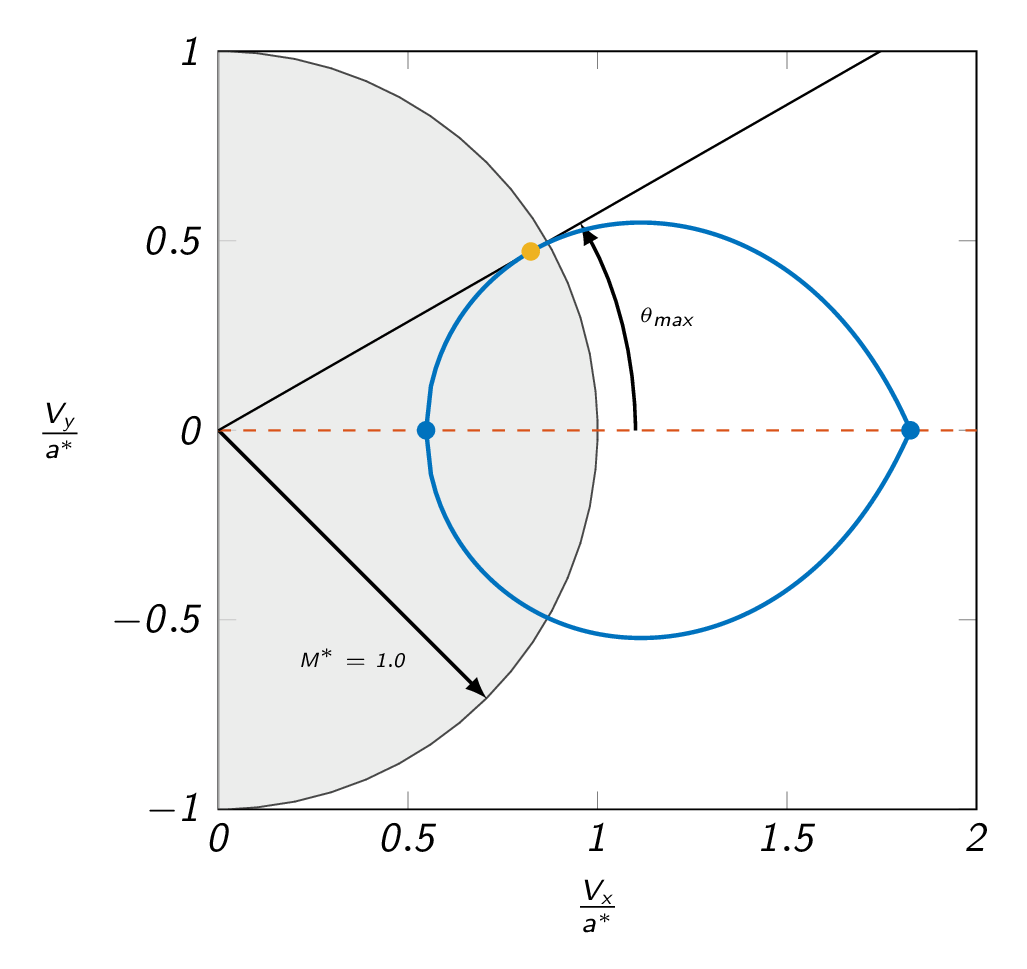
Defining \(V_x\) and \(V_y\) as the cartesian components of the velocity vector downstream of the shock (see figure below), the shock polar gives a graphic representation of all possible solutions for a given Mach number.
The figure below shows a shock polar for a specific Mach number. The gray circle defines the limit for subsonic downstream Mach number. The no deflection cases (the solutions on the x-axis) are the normal shock solution (within the gray circle) and a Mach wave (the right-most solution). As indicated in the figure, there is a maximum deflection angle \((\theta_{max})\). The maximum possible deflection depends on upstream Mach number (each Mach number has its own shock polar).
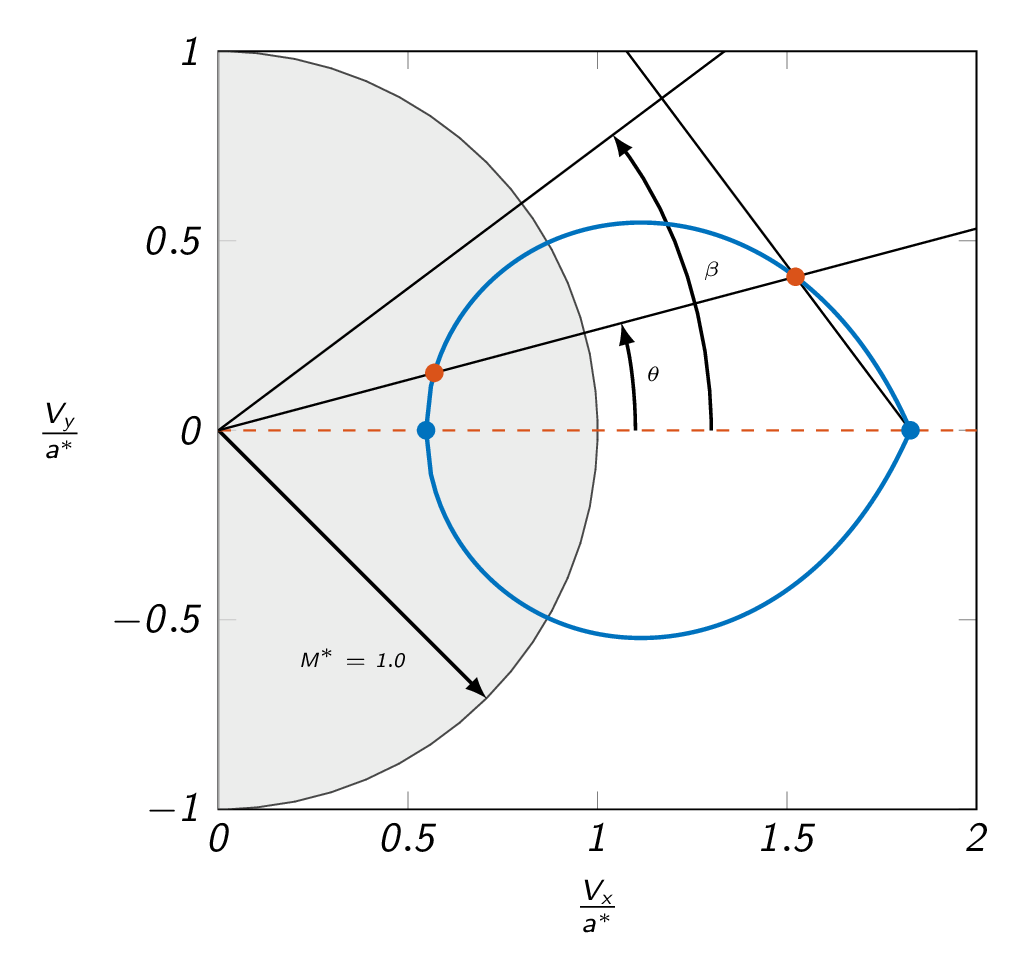
For cases where the flow deflection angle is less than the maximum angle, there are two possible solutions. These are often referred to as the weak and the strong solution, respectively. The strong solution will result in subsonic flow downstream of the shock. The weak solution may give subsonic flow downstream of the shock but most often the flow downstream of a weak shock will be supersonic. The strong solution will always give higher losses than the weak solution and therefore the weak solution will be the preferred solution if possible. The shock angle \(\beta\) can be obtained from the shock polar as indicated in the figure below where the shock angle for the weak solution is obtained using two lines. First a line connecting the Mach wave solution and the weak solution is drawn. Then another line starting at \((V_x,V_y)=(0,0)\) that is perpendicular to the first line will define the shock angle. The shock angle related to the strong solution can be obtained in the same way.
The \(\theta\)-\(\beta\)-Mach Relation
Another way to represent solutions to a oblique shock problem is the \(\theta\)-\(\beta\)-Mach relation given by
$$\tan (\theta)=\frac{2\cot (\beta) (M_1^2 \sin^2 (\beta) -1)}{M_1^2(\gamma + \cos (2 \beta))+2}$$The \(\theta\)-\(\beta\)-Mach relation is shown graphically in the figure below. Each of the blue lines represents a specific upstream Mach number. The peak of a Mach number curve defines the maximum deflection angle \((\theta_{max})\) for that specific Mach number. For deflection angles that fall to the right of \(\theta_{max}\) for a specific Mach number there is no oblique shock solution.
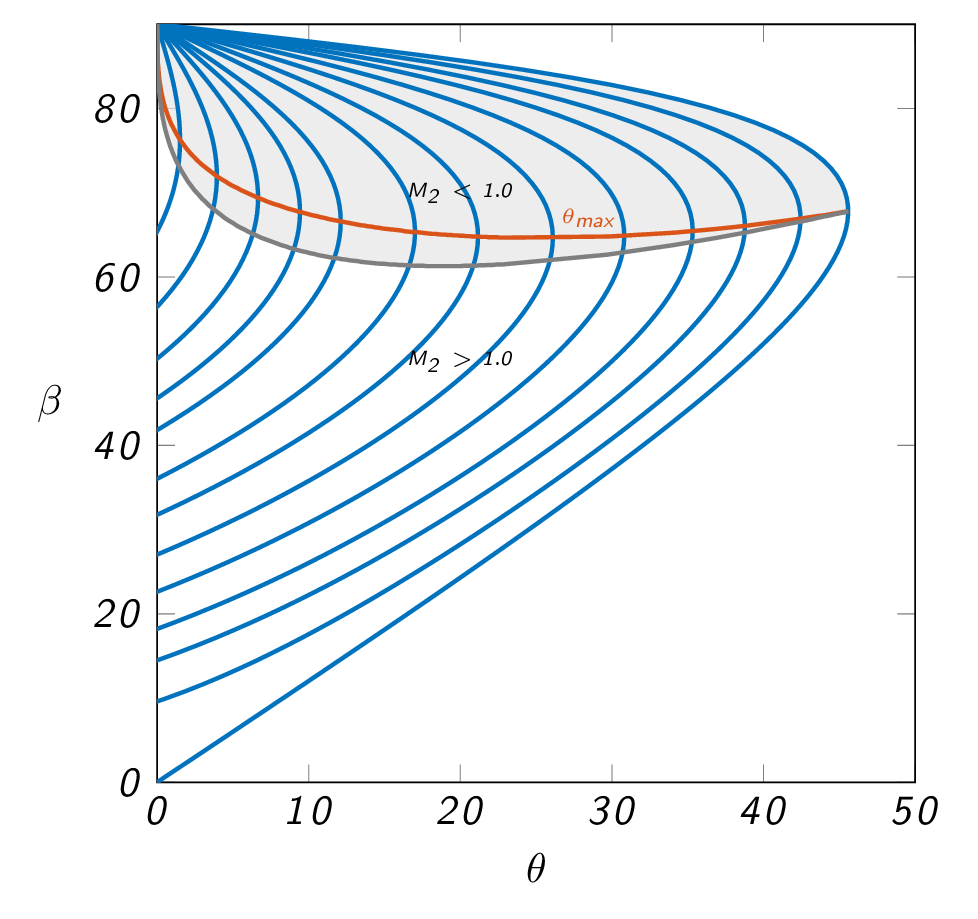
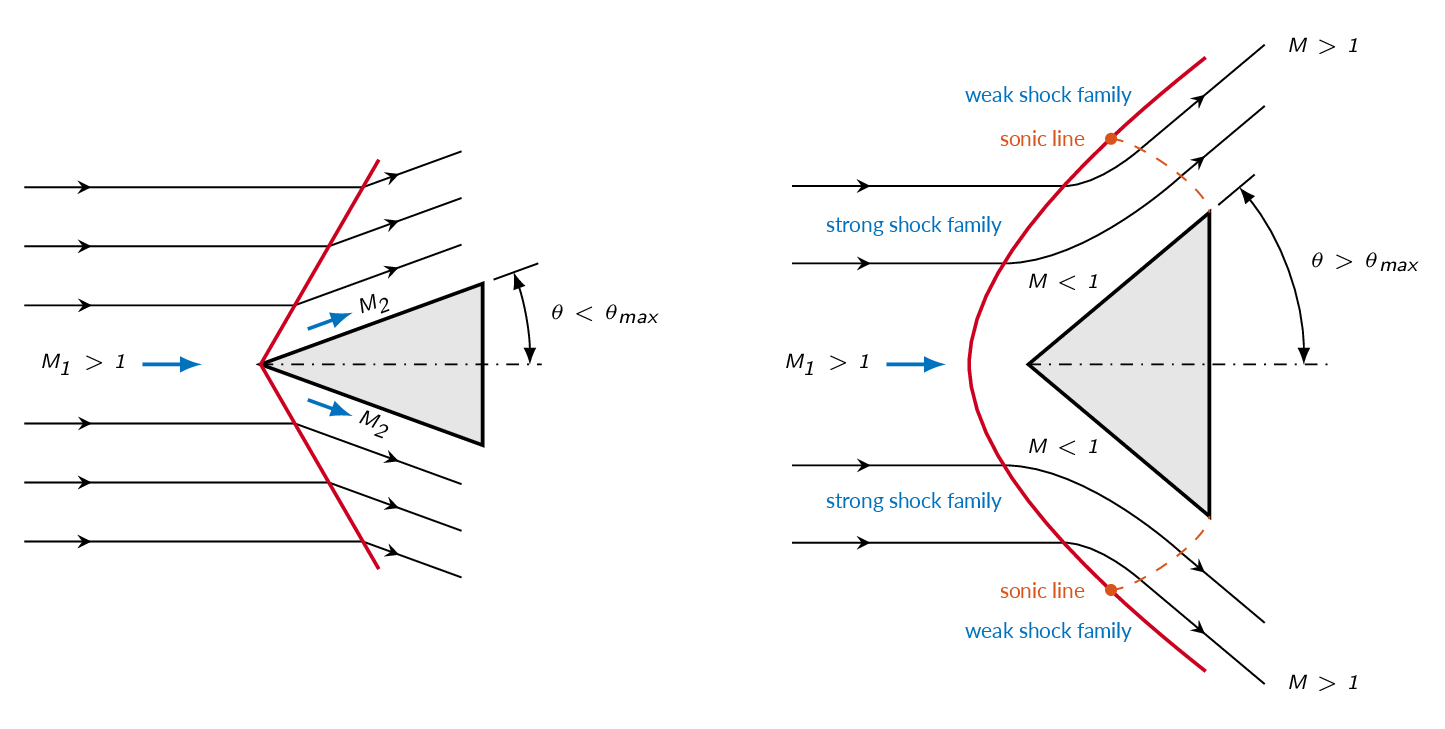
The figure below illustrates schematically what will happen if the deflection angle is smaller than the \(\theta_{max}\) (left figure) and greater than \(\theta_{max}\) (right figure). In the left figure to the left the wedge angle is smaller than \(\theta_{max}\) for the upstream Mach number and an oblique shock will appear at the leading edge of the wedge defined such that the flow is deflected and follows the surface of the wedge. In the right figure the wedge angle is larger than \(\theta_{max}\) and thus an oblique shock solution is impossible. Instead a detached shock will form ahead of the wedge and there will be a region of subsonic flow ahead of the wedge.
Expansion Waves
When the flow direction of a supersonic flow is changed so that the flow is bent into itself, the flow deflection is accomplished by an oblique shock or an compression region. If, on the other hand, the flow needs to bend away from itself, i.e., the flow channel opens up, the flow deflection is accomplished by an expansion region. The expansion region is built up of a large number of Mach waves. Each of these Mach waves is isentropic and results in an infinitesimal flow deflection. The expansion region deflects the flow by accumulation of these infinitesimal deflections and the change in flow properties as the flow passes through the expansion region is isentropic.
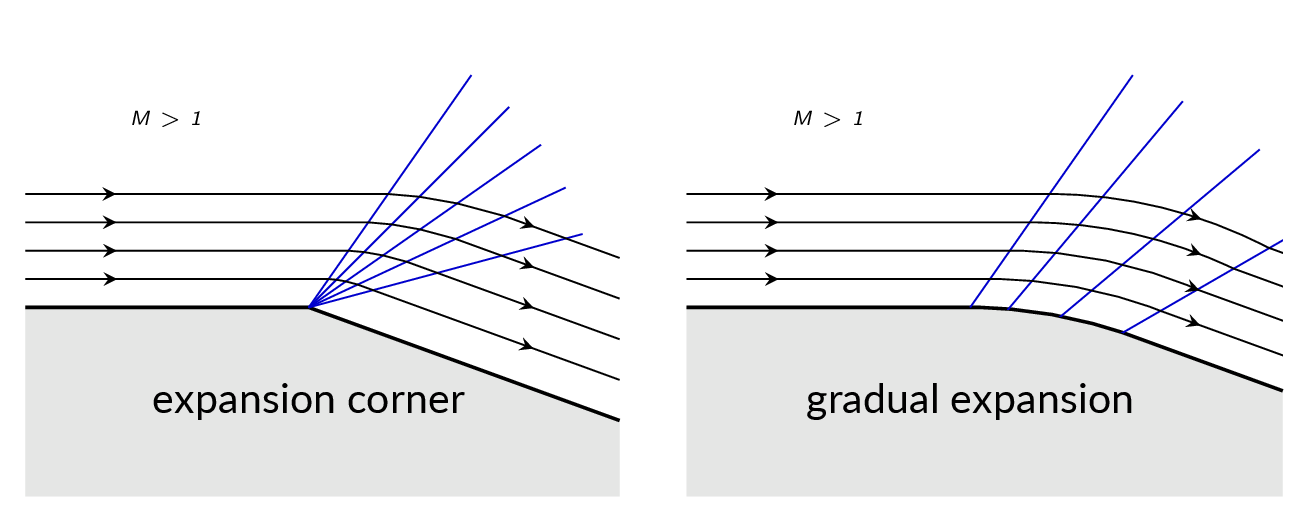
The change of flow properties over an expansion region can be calculated using the Prandtl-Meyer function. The Prandtl-Meyer function derivation is based on the fact that each expansion wave gives an infinitesimal change in flow angle and flow properties.
$$\omega(M)=\left(\frac{\gamma+1}{\gamma-1}\right)^{1/2}\tan^{-1}\left(\frac{M^2-1}{(\gamma+1)/(\gamma-1)}\right)^{1/2}-\tan^{-1}(M^2-1)^{1/2}$$
The flow deflection approaches a maximum flow angle asymptotically and the maximum theoretical flow deflection angle is given by
$$\left.\omega(M)\right|_{M\rightarrow \infty}=130.45^{\circ}$$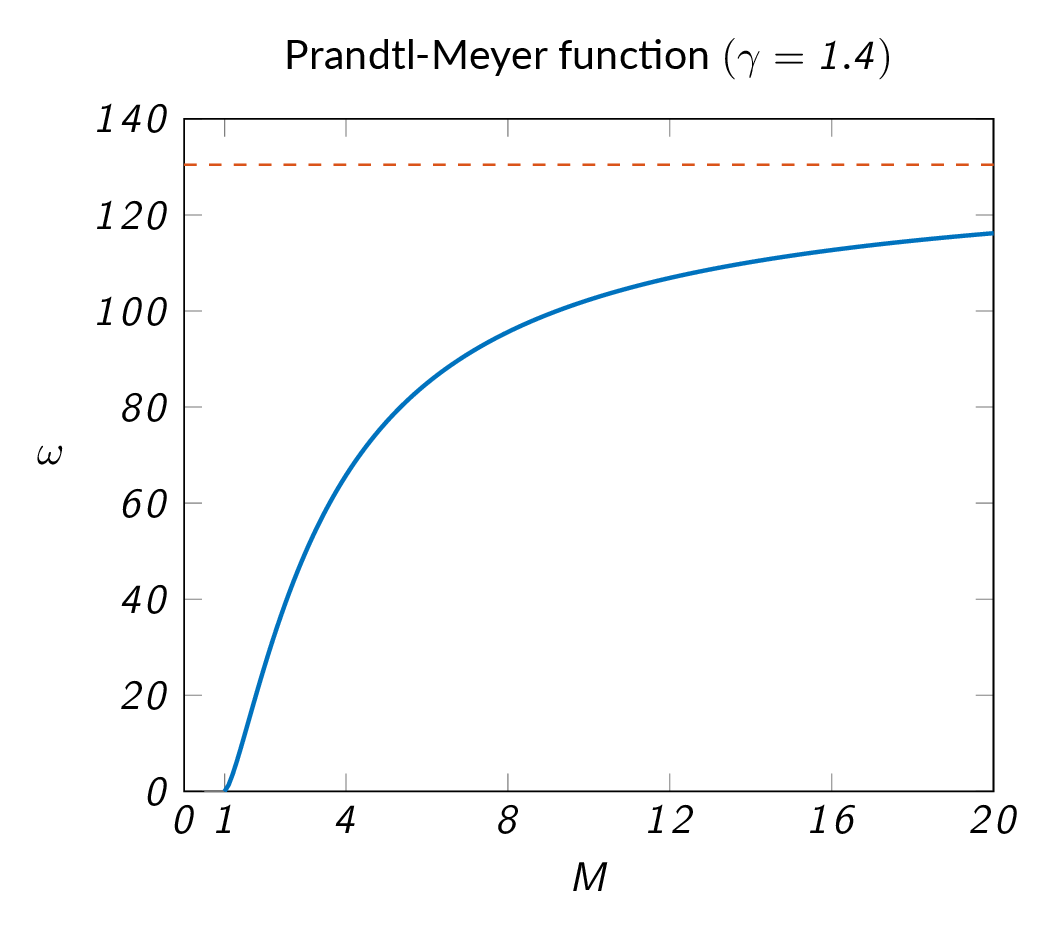
Since the expansion process is isentropic, the isentropic relations can be used.
$$\frac{T_o}{T} =\left[1+\frac{1}{2}(\gamma-1)M^2\right]$$ $$\frac{T_1}{T_2} =\frac{T_{o_2}}{T_{o_1}}\frac{T_1}{T_2}=\left.\left(\frac{T_{o_2}}{T_2}\right)\middle/\left(\frac{T_{o_1}}{T_1}\right)\right.=\left\{T_{o_1}=T_{o_2}\right\}=\left[\frac{1+\frac{1}{2}(\gamma-1)M_2^2}{1+\frac{1}{2}(\gamma-1)M_1^2}\right]$$In the same way
$$\frac{p_o}{p} =\left[1+\frac{1}{2}(\gamma-1)M^2\right]^{\frac{\gamma}{\gamma-1}}$$ $$\frac{p_1}{p_2} =\frac{p_{o_2}}{p_{o_1}}\frac{p_1}{p_2}=\left.\left(\frac{p_{o_2}}{p_2}\right)\middle/\left(\frac{p_{o_1}}{p_1}\right)\right.=\left\{p_{o_1}=p_{o_2}\right\}=\left[\frac{1+\frac{1}{2}(\gamma-1)M_2^2}{1+\frac{1}{2}(\gamma-1)M_1^2}\right]^{\frac{\gamma}{\gamma-1}}$$As the flow passes through the expansion region, there will be an increase of the flow Mach number, the pressure will decrease and the temperature will increase.
Shock-Expansion Theory
Shock expansion theory a collective name for problems including both shocks and expansion regions such as the diamond shaped airfoil and the flat plate at an angle of attack in the figures below. Oblique shock relations and the Prandtl-Meyer expansion theory can be used to calculate the flow states in the different regions in the figures below. Since the diamond-shaped wing in the first of the two figures does not have an angle of attack in relation to the flow and since it is symmetric, the flow will be symmetric. This means that no lift will be generated since the pressures will be the same on the upper and lower side of the wing. There will, however, be a drag force generated since the pressure in region 2 will be higher than the pressure in region 3. The drag that is generated in this case is called wave drag and is associated with the shocks generated at the leading edge of the wing.
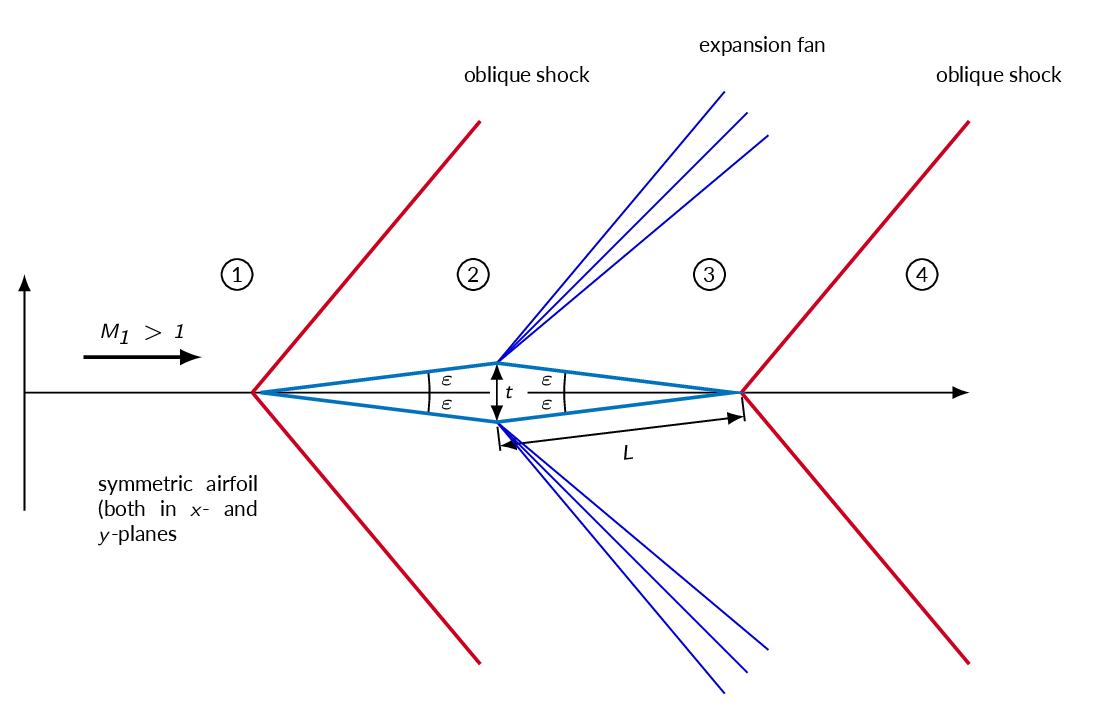
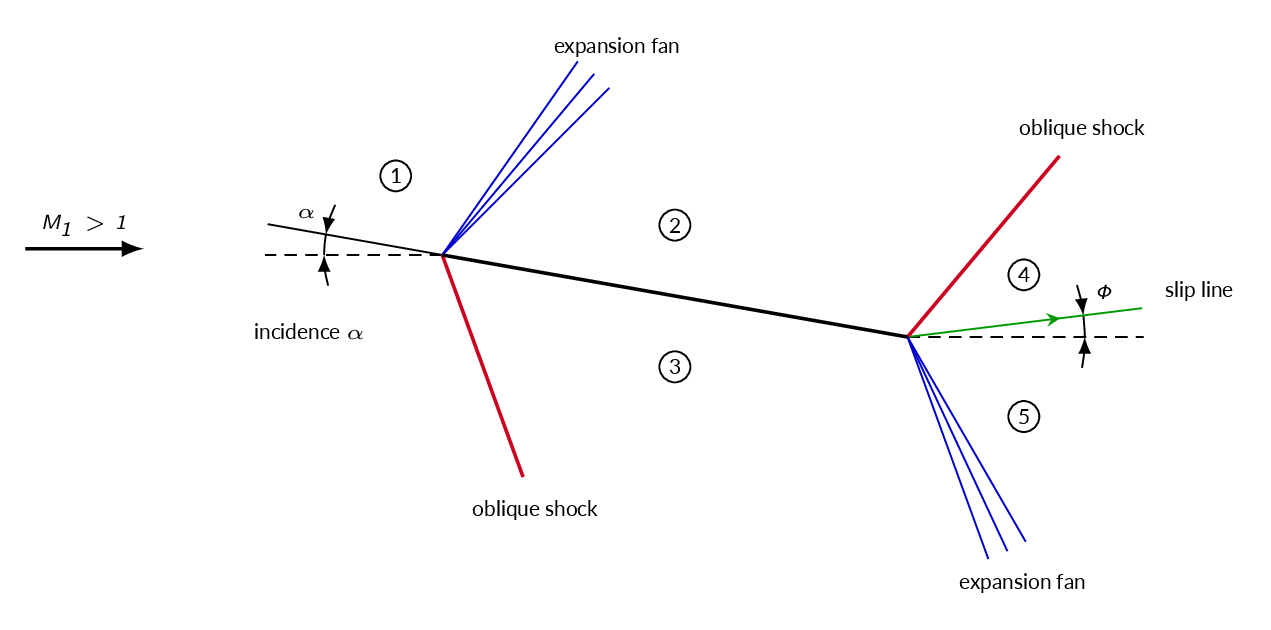
In the figure below, a flat plate is situated in a supersonic freestream. In this case we will get both lift and drag since the flow is not symmetric. An interesting effect of the asymmetric flow is that it is very unlikely that it is possible to match the pressure downstream of the wing without generating a net deflection of the flow.
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
- How is the Mach number defined?
- Show by estimation of the density variation in a fluid flow that the criteria for incompressible flow is \(M\ll1\)
hint: see Eqn 4.13 - 4.17 in White - What is the upper Mach number often used as the limit for incompressible flow?
- Name the different Mach number regimes in compressible flow and specify the corresponding Mach number ranges
- What is an adiabatic process?
- What is required for a process to be isentropic?
- Write down the relation between internal energy and temperature and between enthalpy and temperature for
- an ideal gas with constant specific heats (calorically perfect gas)
- an ideal gas with specific heats that are functions of temperature (thermally perfect gas)
- Derive an expression for the speed of sound for a generic fluid. In the derivation, an assumption regarding the pressure derivative is made -- what is the assumption?
- The speed of sound in a generic fluid is given by $$a=\sqrt{\left(\dfrac{\partial p}{\partial \rho}\right)_s}$$ From the relation above, derive an expression for the speed of sound in a calorically perfect gas (perfect gas with constant specific heats) as a function of temperature. Use the isentropic relation $$\dfrac{p_2}{p_1}=\left(\dfrac{\rho_2}{\rho_1}\right)^\gamma$$
- The adiabatic energy equation
- Write down the energy equation for steady-state adiabatic compressible flow without potential energy changes and no viscous work. The equation should be written out using enthalpy.
- Rewrite the energy equation from the previous question but now expressed in terms of temperature
- Now, derive the following relation: $$\dfrac{T_o}{T}=1+\dfrac{\gamma-1}{2}M^2$$
- Which of the properties \(h_o\), \(T_o\), \(a_o\), \(p_o\), and \(\rho_o\) are constants in a flow if the flow is adiabatic and isentropic, respectively?
- What is a critical property (such as for example the critical temperature \(T^\ast\)?
- Using the continuity equation and energy equation on differential form together with the definition of speed of sound, the following relation can be derived $$\dfrac{dV}{V}=\dfrac{dA}{A}\dfrac{1}{M^2-1}=-\dfrac{dp}{\rho V^2}$$ Show, using the relation given above, how the velocity and pressure changes in a flow through a divergent or convergent duct for initially subsonic flow or initially supersonic flow
- Explain the concept of choking
- Normal shocks:
- Explain what a normal shock is. What happens with the velocity, pressure and total temperature over a normal shock? How is the critical area, \(A^\ast\) effected?
- The normal shock equation system has two solutions. How do we know which solution that is the correct one? %What is the implication of this for very weak waves (such as for example acoustic/sound waves)?
- How is the Hugoniot relation derived?
- Derive a relation for the pressure ratio over a normal shock
- How does pressure (\(p\)), temperature (\(T\)), density (\(\rho\)), Mach number (\(M\)), total pressure (\(p_o\)), and total temperature (\(T_o\)) change over a normal shock?
- Explain, using a schematic figure, how pressure and velocity varies in a nozzle (the two types of nozzles specified below) as the downstream pressures (back pressures) changes. The upstream end of the nozzle is connected to a large reservoir (tank) with the pressure \(p_o\) and temperature \(T_o\). What happens with the mass flow when the downstream pressure changes?
- convergent nozzle
- convergent-divergent nozzle
- Make a schematic sketch showing how pressure waves expands around an object moving at
- subsonic speed
- sonic speed
- supersonic speed
- Oblique shocks:
- Show schematically how the velocity (normal velocity component, tangential velocity component, and the total velocity) changes over an oblique shock. Indicate the shock angle, \(\beta\), and the deflection angle, \(\theta\).
- Show schematically how the oblique shock formed ahead of a wedge traveling at supersonic speed if
- \(\theta<\theta_{max}\)
- \(\theta>\theta_{max}\)
- Can the relations for total quantities for a normal shock be used for an oblique shock? Explain why/why not.
- Prandtl-Meyer expansions:
- What is a Prandtl-Meyer expansion. Show with a figure.
- How does pressure (\(p\)), temperature (\(T\)), density (\(\rho\)), Mach number (\(M\)), total pressure (\(p_o\)), and total temperature (\(T_o\)) change over an expansion region?
| Document Archive | ||
| MTF053_C09.pdf | lecture notes chapter 9 | |
| MTF053_Compressible-Flow-Hugoniot-Equation.pdf | Complementary material - Derivation of the Hugoniot equation - a relation of thermodynamic properties over a normal shock | |
| MTF053_Formulas-Tables-and-Graphs.pdf | A collection of formulas, tables, and graphs | |
| MTF053_Study-Guide.pdf | A collection of theory questions that give a good representation of the theory covered in the course | |