Chapter 1
Introduction to Fluid Mechanics
Introduction to Fluid Mechanics
Overview
The first chapter gives an introduction to fluid mechanics and basic concepts such as the continuum assumption and fluid viscosity are introduced.
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them. It has applications in a wide range of disciplines, including mechanical, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology.
When you think about it, almost everything on this planet either is a fluid or moves within or near a fluid
Roadmap
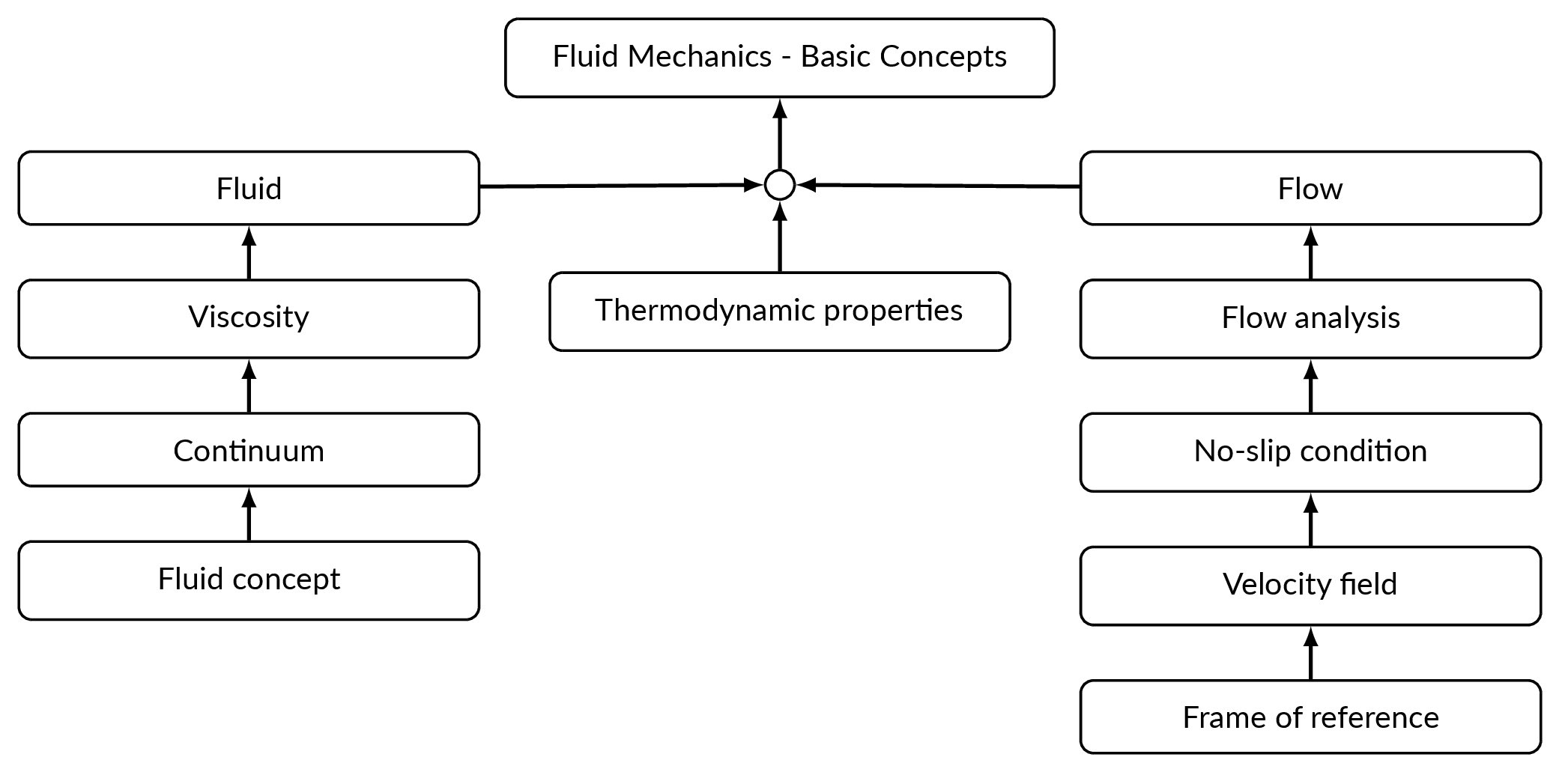
The Fluid Concept
In physics, a fluid is a substance that continually deforms (flows) under an applied shear stress, or external force. Fluids are a phase of matter and include liquids, gases and plasmas. They are substances with zero shear modulus, or, in simpler terms, substances which cannot resist any shear force applied to them.

A solid can resist a shear stress by a static deflection; a fluid cannot.
The Continuum Assumption
To be able to use differential calculus in the analysis of fluid flows, fluid properties must be continuous. The continuum assumption means that fluid volumes are studied that are large enough to ensure that the number of fluid molecules within the volume is about constant and small enough to not introduce macroscopic fluctuations. The figure below illustrates how fluid density varies width volume size. If the volume of fluid parcels are within the range for which the continuum assumption applies, the number of molecules within the volume does not vary significantly and the density is constant.
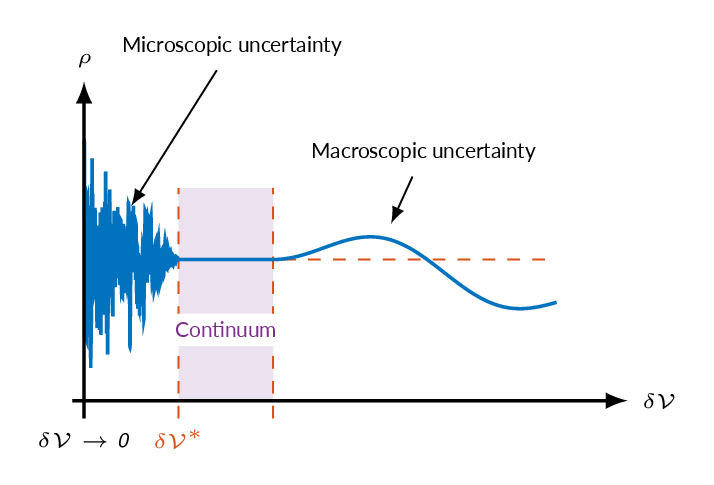 $$\rho=\lim_{\delta \mathcal{V} \rightarrow \delta \mathcal{V}^*}\frac{\delta m}{\delta \mathcal{V}}$$
$$\rho=\lim_{\delta \mathcal{V} \rightarrow \delta \mathcal{V}^*}\frac{\delta m}{\delta \mathcal{V}}$$
Standard air: \(\delta \mathcal{V^\ast} \approx 10^{-9}mm^3\Rightarrow \sim 3\times 10^7\) molecules
Frame of Reference
Eulerian frame of reference
- fluid properties are functions of position and time
- most often used in fluid mechanics
Lagrangian frame of reference
- follows a system (a collection of matter of fixed identity) in time and space
- can be used in fluid mechanics
- most often used in solid mechanics
Properties of the Velocity Field
The fluid velocity is a function of position and time. The velocity components in the \(x\), \(y\), and \(z\) directions are denoted \(u\), \(v\), and \(w\), respectively.
$$\mathbf{V}(x,y,z,t)=u(x,y,z,t)\mathbf{e}_x+v(x,y,z,t)\mathbf{e}_y+w(x,y,z,t)\mathbf{e}_z$$The acceleration vector is obtained according to
$$\mathbf{a}=\frac{d\mathbf{V}}{dt}=\frac{\partial\mathbf{V}}{\partial t}+\left(\frac{\partial \mathbf{V}}{\partial x}\right)\left(\frac{\partial x}{\partial t}\right)+\left(\frac{\partial \mathbf{V}}{\partial y}\right)\left(\frac{\partial y}{\partial t}\right)+\left(\frac{\partial \mathbf{V}}{\partial z}\right)\left(\frac{\partial z}{\partial t}\right)$$$$\frac{d\mathbf{V}}{dt}=\frac{\partial\mathbf{V}}{\partial t}+{\color{MatlabA}{u}}\frac{\partial \mathbf{V}}{\partial x}+{\color{MatlabB}{v}}\frac{\partial \mathbf{V}}{\partial y}+{\color{MatlabD}{w}}\frac{\partial \mathbf{V}}{\partial z}$$
Thermodynamic Properties
Thermodynamic properties describe the state of a system, i.e., a collection of matter of fixed identity which interacts with its surroundings. The system is a small fluid element, and all properties are continuum properties of the flow field. For a single-phase substance, two basic thermodynamic properties are sufficient to get the values of all other thermodynamic properties.
Most common properties
- Pressure \(p\) \([Pa]\)
- the compression stress at a point in a static fluid
- a fluid flow is often driven by pressure gradients
- if the pressure drops below the vapor pressure in a liquid, vapor bubbles will form
- Density \(\rho\) \([kg/m^3]\)
- mass per unit volume
- nearly constant in liquids (incompressible) - for water, the density increases about one percent for a pressure increase by a factor of 220
- not constant for gases
- Temperature \(T\) \([K]\)
- related to internal energy
- large temperature differences \(\Rightarrow\) heat transfer may be important
Work, heat, and energy balances
- Internal energy \(\hat{u}\)
- Enthalpy \(h=\hat{u}+p/\rho\)
- Entropy \(s\)
- Specific heats \(C_p\) and \(C_v\)
Friction and heat conduction
- Viscosity \(\mu\)
- Thermal conductivity \(k\)
Fluid Energy
The fluid energy per unit mass is given by
$$e=\hat{u}+\frac{1}{2}V^2+gz$$where \(\hat{u}\) is the internal energy of the fluid, which is a function of temperature. The potential and kinetic energies are kinematic quantities.
State relation for gases
The perfect gas law:
$$p=\rho R T$$where \(R\) is the gas constant
$$R=C_p-C_v$$The perfect gas law requires: \(\hat{u}=\hat{u}(T)\) and thus
$$C_v=\left(\frac{\partial \hat{u}}{\partial T}\right)_\rho=\frac{d\hat{u}}{dT}=C_v(T)$$specific heat (constant pressure):
$$h=\hat{u}+\frac{p}{\rho}=\hat{u}+RT=h(T)$$ $$C_p=\left(\frac{\partial h}{\partial T}\right)_p=\frac{dh}{dT}=C_p(T)$$ratio of specific heats:
$$\gamma=\frac{C_p}{C_v}\ge1$$From the definition of the gas constant \(R\) and the ratio of specific heats \(\gamma\), we get
$$C_v=\frac{R}{\gamma-1}$$ $$C_p=\frac{\gamma R}{\gamma-1}$$Speed of sound
Speed of sound plays an important role when compressible effects are important (Chapter 9)
$$a^2=\left(\frac{\partial p}{\partial \rho}\right)_s$$ $$\tau_s=\frac{1}{\rho}\left(\frac{\partial \rho}{\partial p}\right)_s\Rightarrow a=\sqrt{\frac{1}{\rho \tau_s}}$$where \(\tau_s\) is the fluid compressibility.
for an ideal gas, one can show that
$$a=\sqrt{\gamma R T}$$Vapor Pressure
Vapor Pressure is the pressure at which a liquid boils and is in equilibrium with its own vapor. If the pressure in a liquid gets lower than the vapor pressure, vapor bubbles will appear in the liquid. If the pressure drops below the vapor pressure due to the flow itself we get cavitation.
Fluid Viscosity
relates the local stresses in a moving fluid to the strain rate of the fluid element
a quantitative measure of the fluid's resistance to flow
For a fluid element sheared in one plane by a single shear stress \(\tau\) such as a fluid particle inside of a boundary layer, as depicted in the figure below, the shear strain angle \(\delta \theta\) will grow continuously over time. Common fluids such as water, oil, and air shows a linear relation between applied shear and the resulting strain rate.
$$\tau \propto \frac{\delta \theta}{\delta t},\ \tan \delta \theta=\frac{\delta u \delta t}{\delta y}\Rightarrow\{\text{small angles} \Rightarrow \tan \delta \theta \approx \delta \theta\}\Rightarrow \tau \propto \frac{\delta u}{\delta y}$$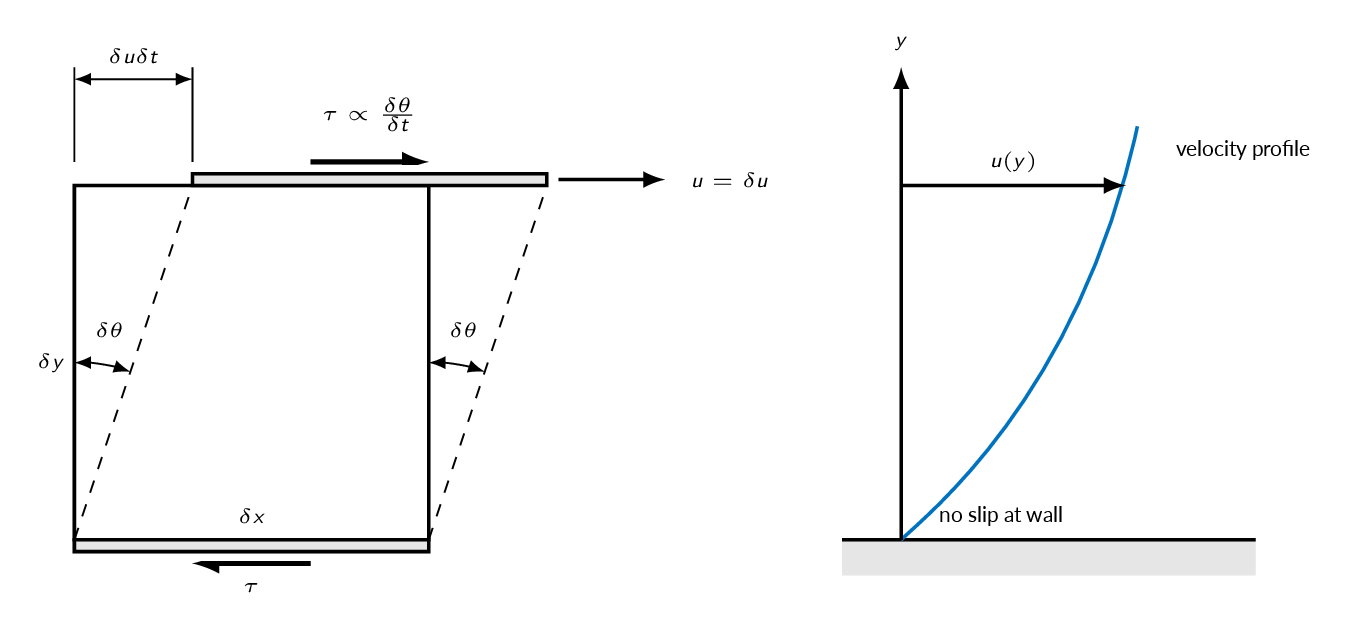
For newtonian fluids
$$\tau=\mu\frac{d\theta}{dt}=\mu\frac{du}{dy}$$where \(\mu\) is the fluid viscosity
Viscosity variation with temperature
Liquids have high viscosity that decreases with temperature since inter-molecular forces decreases with temperature while gases have low viscosity that increases with temperature due to increased molecular movement.
The Reynolds Number
$$Re=\frac{\rho V L}{\mu}$$- Non-dimensional number that relates viscous forces to inertial forces
- Very important parameter in fluid mechanics
- \(V\) and \(L\) are characteristic velocity and length scales of the flow
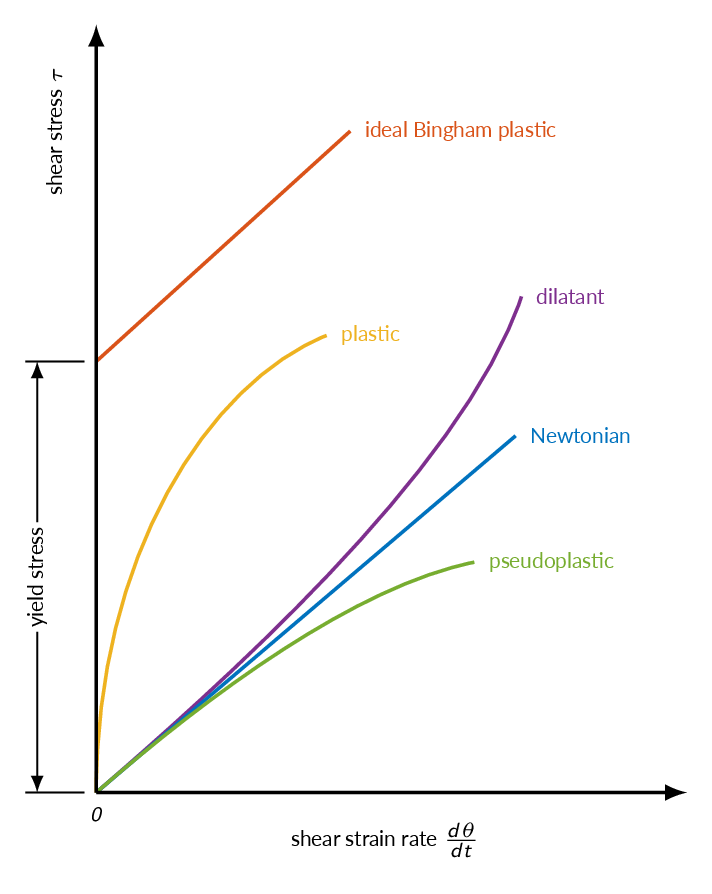
Non-Newtonian Fluids
Non-Newtonian fluids are fluids for which shear stress is not a linear function of strain rate
- Dilatant - shear thickening:
increases resistance to flow with increasing strain rate
Examples: corn starch or sand in water - Pseudoplastic - shear thinning:
decreased resistance to flow with increasing strain rate
Examples: paint and blood plsasma - Bingham plastic:
requires an initial yield stress before starting to flow
Examples: ketchup and toothpaste
The No-slip Condition
At a solid wall, the fluid will have the velocity and temperature of the wall
When a fluid flow is bounded by a solid surface, molecular interactions cause the fluid in contact with the surface to seek momentum and energy equilibrium with that surface
Flow Visualization
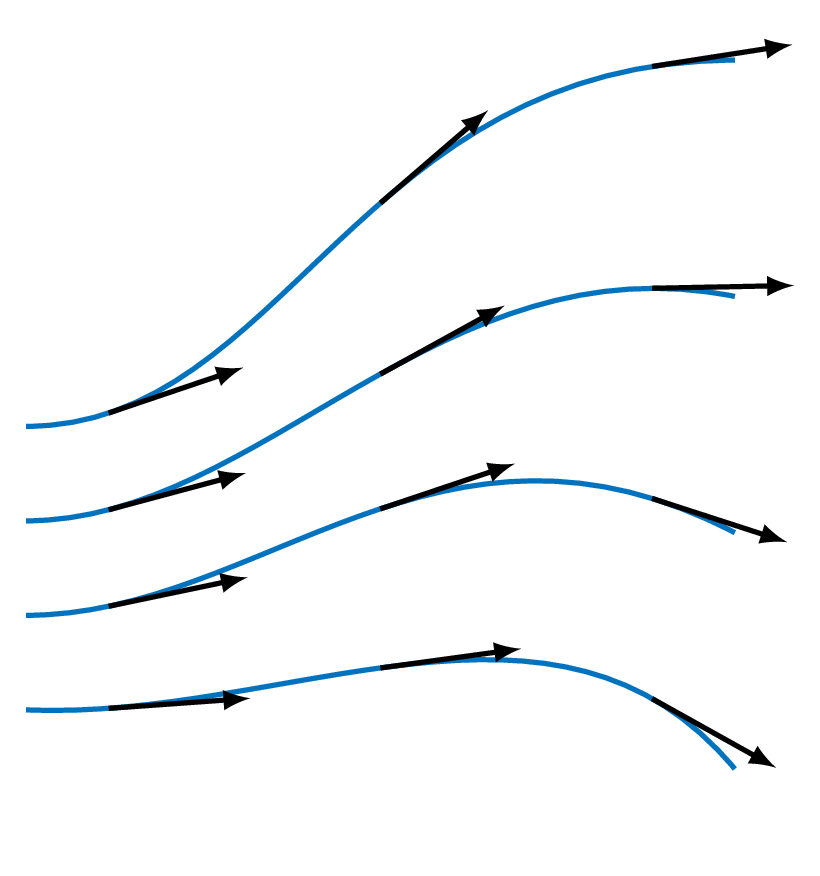
- Streamline (figure below)
a line that is tangent to the velocity vector everywhere at an instant in time - Pathline
the actual path traversed by a fluid particle - Streakline
the locus of particles that have earlier passed through a prescribed point - Timeline
a line formed by a set of particles at a given instant
Note! In a steady-state flow, streamlines, pathlines and streaklines are identical
The figure below, compares streamlines, pathlines, and streaklines for a made up example where the direction of the flow changes abruptly.
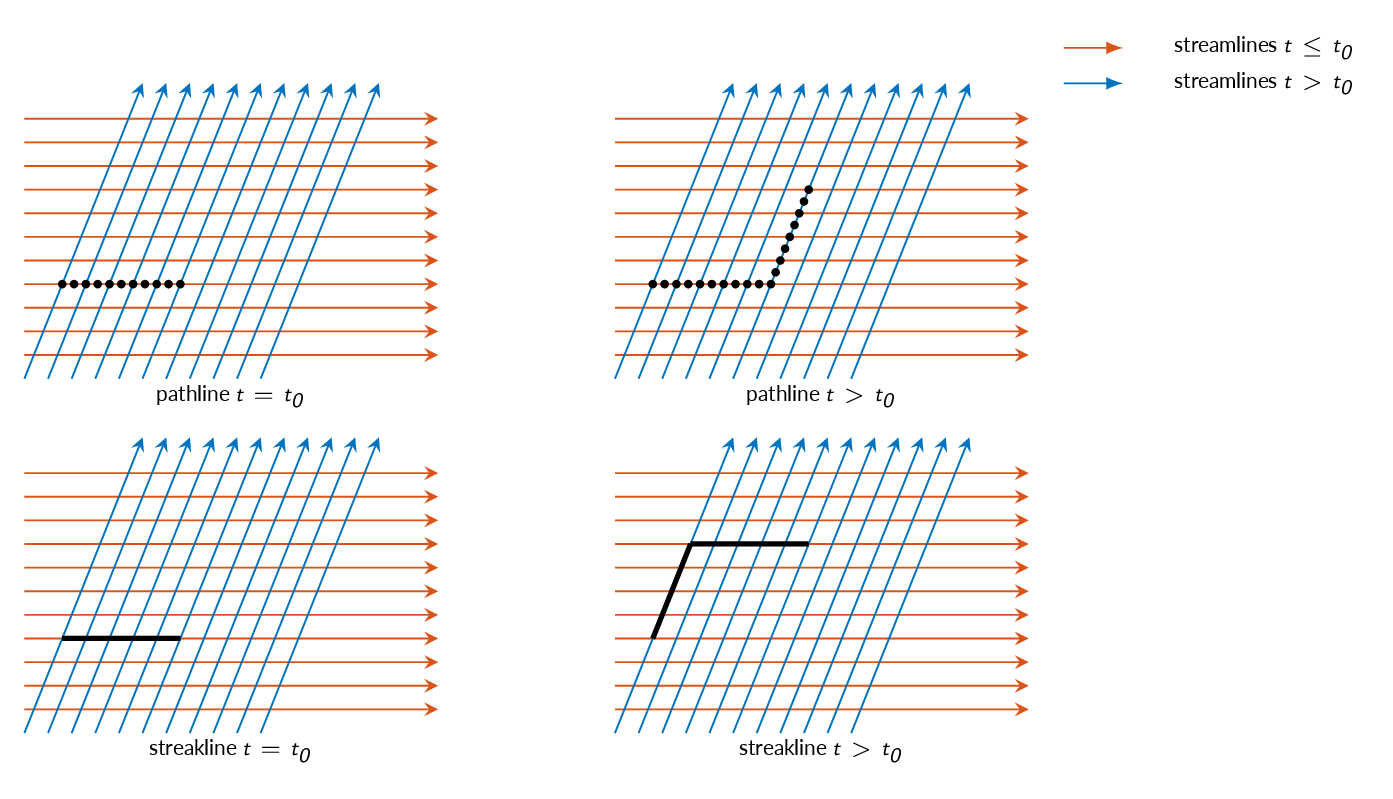
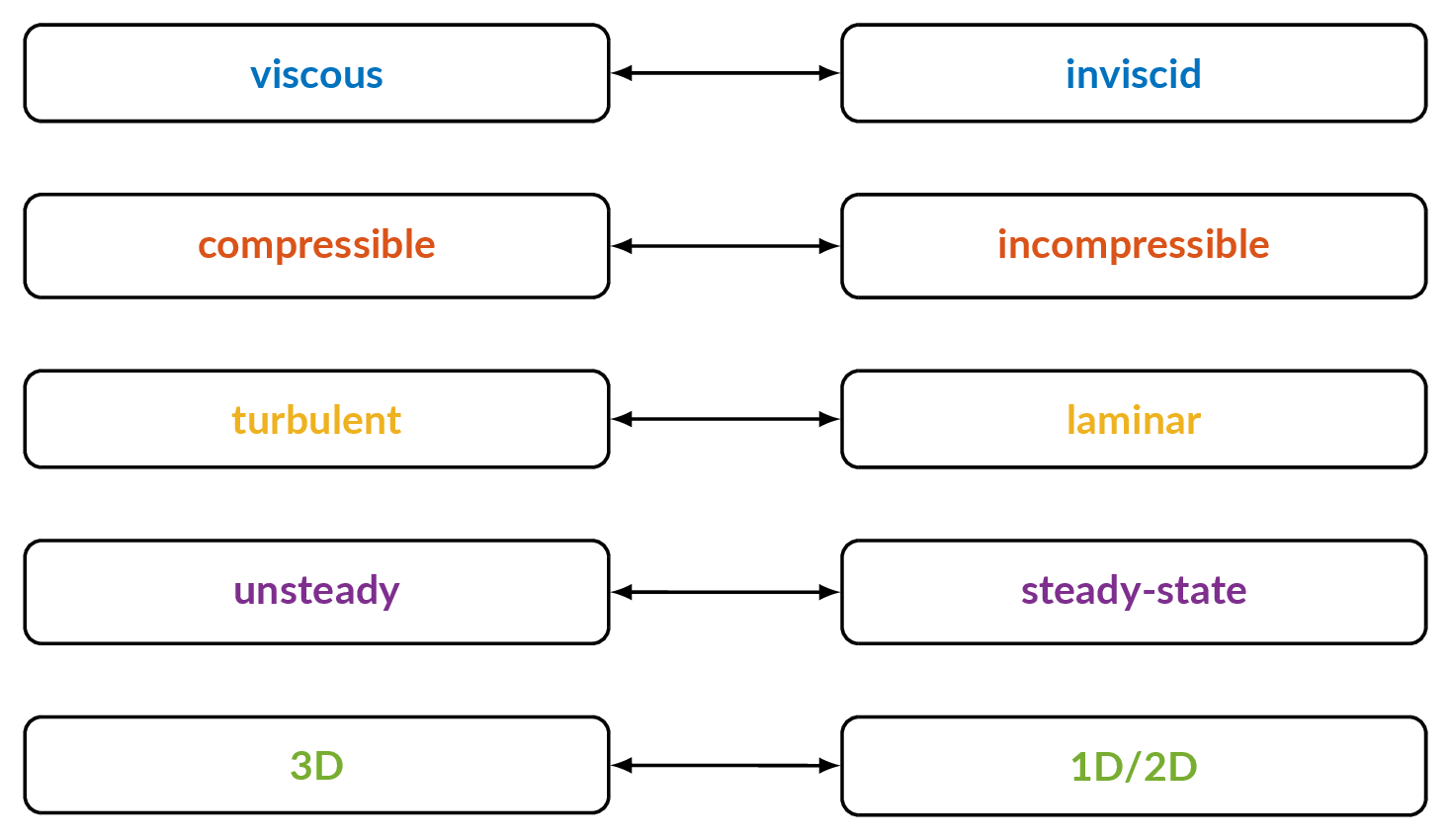
Classification of Fluid Flows
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
- Explain how a fluid differs from a solid. How does a fluid element and solid element react under the presence of shear forces?
- The continuum concept is very central in fluid mechanics - explain this concept.
- Primary and secondary dimensions:
- What does primary dimension mean?
- Which are the primary dimensions used in fluid mechanics?
- Give examples of secondary dimensions.
- What does a dimensional homogeneous equation imply?
- Explain the difference between Eulerian and Lagrangian frame of reference
- Show that if the shear stress is proportional to the fluid element strain rate \(\delta \theta /\delta t\), it is also proportional to the velocity gradient \(du/dy\)
- What is the viscosity of a fluid?
- For a viscous flow, what is the fluid velocity at a wall? What is this boundary condition called?
- What does it mean that a fluid is Newtonian?
- How is the Reynolds number defined? Explain in words what the Reynolds number is.
- Explain the following concepts:
- Steady-state flow
- Unsteady flow
- Incompressible flow
- Inviscid flow
- Turbulent flow
- What is the vapor pressure of a fluid? Explain why cavitation may occur if the pressure becomes low enough in a fluid flow
- Explain the difference between streamline, pathline, and streakline. Under what circumstances do these three line types coincide in a fluid flow?
- The energy per unit mass \(e\) can be expressed as follows: $$e=\hat{u}+\dfrac{1}{2}V^2+gz$$ The three components on the right-hand side represents different forms of energy what does each of the terms represent physically?
- How does the fluid viscosity vary with temperature in liquids and gases, respectively.
| Document Archive | ||
| MTF053_C01.pdf | Lecture notes chapter 1 | |
| MTF053_Formulas-Tables-and-Graphs.pdf | A collection of formulas, tables, and graphs | |
| MTF053_Study-Guide.pdf | A collection of theory questions that give a good representation of the theory covered in the course | |