Chapter 5
Dimensional Analysis and Similarity
Dimensional Analysis and Similarity
Overview
Chapter 5 discusses the importance of non-dimensional groups in the analysis of fluid flow data. The Buckingham \(\Pi\)-theorem, a systematic tool for identification of non-dimensional groups for a specific problem is presented and the concepts geometric, kinematic and dynamic similarity are introduced. Moreover, the non-dimensional form of the Navier-Stokes equations are derived in this chapter. The non-dimensional flow equations plays a central role in the establishment of the boundary-layer equations and will be discussed further in chapter 7.
Roadmap
Dimensional Analysis
Most practical fluid flow problems are too complex, both geometrically and physically, to be solved analytically. They must be tested by experiments or approximated by CFD
Why dimensional analysis?
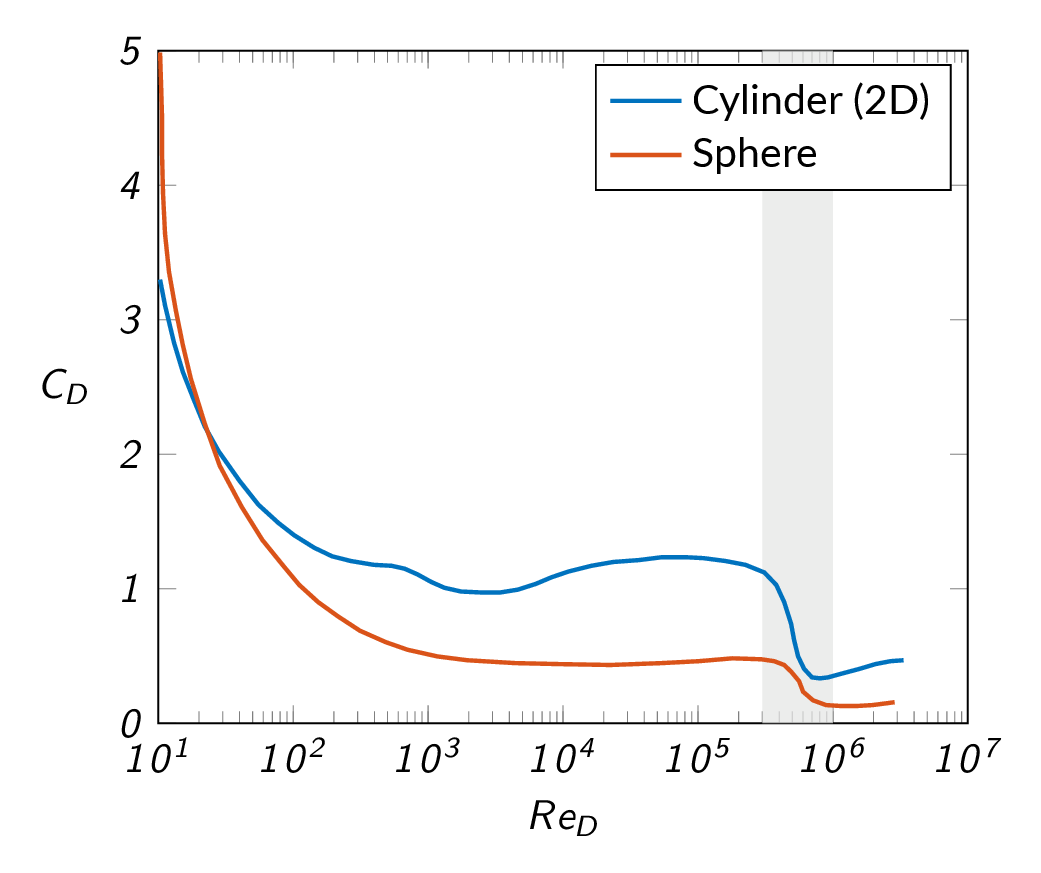
- Large data sets may be represented by a few curves or even a single curve. As an example the figure below, which represents drag coefficient for cylinders and spheres as a function of Reynolds number and is generated from data obtained from a large number of experiments.
- Dimensional analysis is a systematic tool for data reduction
- Experimental/simulation data are more general in non-dimensional form
- Gives insight into physical relationships
- Helps in identifying important and unimportant parameters for a specific problem
- Provides scaling laws - convert data from model-scale to prototype-scale
The Buckingham \(\Pi\)-theorem
If there is a physically meaningful equation involving a certain number \(n\) of physical variables, then the original equation can be rewritten in terms of a set of \(k\) dimensionless parameters \(\Pi_1\), \(\Pi_2\), ..., \(\Pi_k\). The reduction \(j=n-k\) equals the number of variables that do not form a \(\Pi\) group among themselves and is always less than or equal to the number of physical dimensions involved
Systematic identification of \(\Pi\) groups:
- List and count the number of variables in the problem \(n\)
- List the dimensions for each of the \(n\) variables
- Find the reduction \(j\)
- initial guess: \(j\) equals the number of dimensions
- look for \(j\) variables that do not form a \(\Pi\)
- if not possible reduce \(j\) by one and start over
- Select \(j\) scaling parameters
- Add one of the other variables to your \(j\) repeating variables and form a power product
- Algebraically, find exponents that make the product dimensionless
An example is provided in the lecture notes: MTF053_C05.pdf
Non-dimensionalized Equations
The non-dimensional form of the flow equations will be discussed in detail in chapter 7.
Dimensionless Groups
| parameter | definition | interpretation | importance |
| Reynolds number | \(Re=\dfrac{\rho UL}{\mu}\) | \(\dfrac{\text{inertia}}{\text{viscosity}}\) | almost always |
| Mach number | \(M=\dfrac{U}{a}\) | \(\dfrac{\text{kinetic energy}}{\text{internal energy}}\) | compressible flow |
| Froude number | \(Fr=\dfrac{U^2}{gL}\) | \(\dfrac{\text{inertia}}{\text{gravity}}\) | free-surface flow |
| Weber number | \(We=\dfrac{\rho U^2 L}{\Upsilon}\) | \(\dfrac{\text{inertia}}{\text{surface tension}}\) | free-surface flow |
| Prandtl number | \(Pr=\dfrac{\mu C_p}{k}\) | \(\dfrac{\text{dissipation}}{\text{conduction}}\) | heat convection |
| specific heat ratio | \(\gamma=\dfrac{C_p}{C_v}\) | \(\dfrac{\text{enthalpy}}{\text{internal energy}}\) | compressible flow |
| Strouhal number | \(St=\dfrac{\omega L}{U}\) | \(\dfrac{\text{oscillation}}{\text{mean speed}}\) | oscillating flow |
| roughness ratio | \(\dfrac{\varepsilon}{L}\) | \(\dfrac{\text{wall roughness}}{\text{body length}}\) | turbulent flow |
| pressure coefficient | \(C_p=\dfrac{p-p_\infty}{0.5\rho U^2}\) | \(\dfrac{\text{static pressure}}{\text{dynamic pressure}}\) | aerodynamics |
| lift coefficient | \(C_L=\dfrac{F_L}{0.5\rho U^2 A}\) | \(\dfrac{\text{lift force}}{\text{dynamic force}}\) | aerodynamics |
| drag coefficient | \(C_D=\dfrac{F_D}{0.5\rho U^2 A}\) | \(\dfrac{\text{drag force}}{\text{dynamic force}}\) | aerodynamics |
| skin friction coefficient | \(C_f=\dfrac{\tau_{wall}}{0.5\rho U^2}\) | \(\dfrac{\text{wall shear stress}}{\text{dynamic pressure}}\) | boundary layers |
Modeling and Similarity
Flow conditions for a model test are completely similar if all relevant dimensionless parameters have the same corresponding values for the model and the prototype
A model and prototype are geometrically similar if and only if all body dimensions in all three coordinates have the same linear-scale ratio
All angles are preserved in geometric similarity. All flow directions are preserved. The orientations of model and prototype with respect to the surroundings must be identical
Geometric Similarity
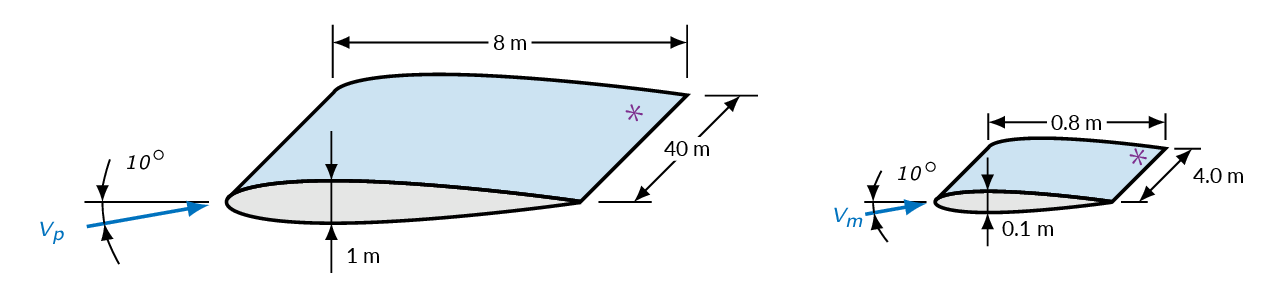
- all dimensions should be scaled with the same linear scaling ratio
- angle of attach should be the same
- scaled nose radius
- scaled surface roughness
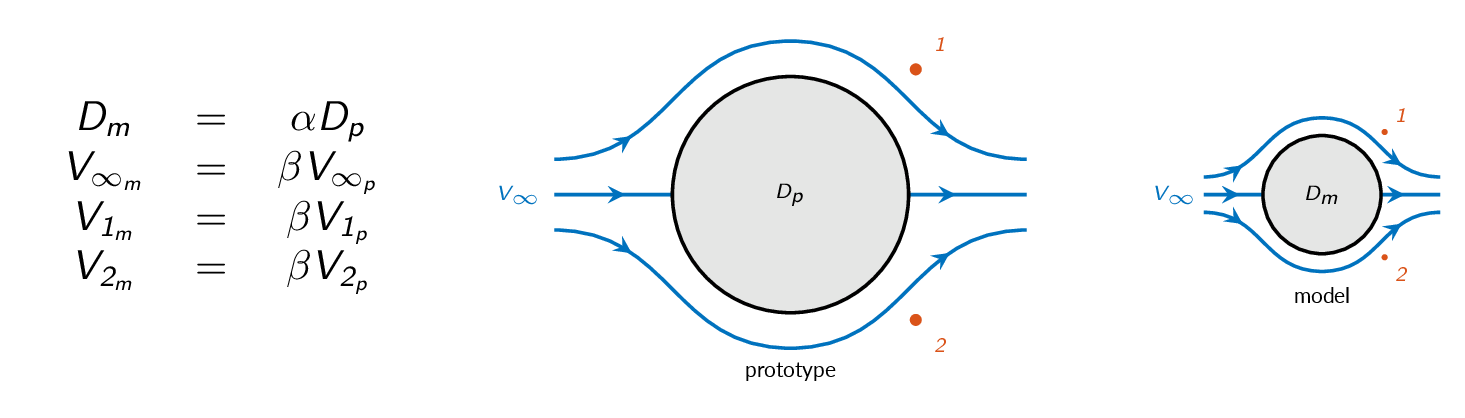
Kinematic Similarity
The motions of two systems are kinematically similar if homologous particles lie at homologous points at homologous times
Incompressible frictionless low-speed flows without free surfaces are kinematically similar with independent length and time scales
Dynamic Similarity
Dynamic similarity is achieved when the model and prototype have the same length scale ratio, time scale ratio, and force scale ratio
- Compressible flow:
- Reynolds number equivalence
- Mach number equivalence
- specific-heat ratio equivalence
- Incompressible flow without free surfaces:
- Reynolds number equivalence
- Incompressible flow with free surfaces:
- Reynolds number equivalence
- Froude number equivalence (and if necessary Weber number and/or cavitation number)
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
- If you are going to do an experimental investigation of a problem including a number of important physical variables, why is it beneficial to divide the variables into non-dimensional groups?
- Rewrite the continuity equation and the \(x\)-component of the momentum equation in non-dimensional form $$\dfrac{\partial u}{\partial x}+\dfrac{\partial v}{\partial y}+\dfrac{\partial w}{\partial z}=0$$ $$\dfrac{\partial u}{\partial t}+u\dfrac{\partial u}{\partial x}+v\dfrac{\partial u}{\partial y}+w\dfrac{\partial u}{\partial z}=g_x-\dfrac{1}{\rho}\dfrac{\partial p}{\partial x}+\dfrac{\mu}{\rho}\left(\dfrac{\partial^2u}{\partial x^2}+\dfrac{\partial^2u}{\partial y^2}+\dfrac{\partial^2u}{\partial z^2}\right)$$
- The flow resistance \(F_D\) of a body immersed in a flow can be divided into pressure forces and friction forces (MTF053 Dimensional-Analysis-and-Similarity.pdf)
- Show using Reynolds similarity that the pressure forces can be written as $$F_{D_p}=C_{D_p}(Re)A_p\dfrac{\rho U^2}{2}$$ where the drag coefficient \(C_{D_p}\) is a function of the Reynolds number only and \(A_p\) is the projected area of the body.
- Show using Reynolds similarity that the pressure forces can be written as $$F_{D_f}=C_{D_f}(Re)A_p\dfrac{\rho U^2}{2}$$ where the drag coefficient \(C_{D_f}\) is a function of the Reynolds number only and \(A_p\) is the projected area of the body.
- Explain the concepts geometric similarity, kinematic similarity, and dynamic similarity
| Document Archive | ||
| MTF053_C05.pdf | Lecture notes chapter 5 | |
| MTF053_Dimensional-Analysis-and-Similarity.pdf | Complementary material | |
| MTF053_Formulas-Tables-and-Graphs.pdf | A collection of formulas, tables, and graphs | |
| MTF053_Study-Guide.pdf | A collection of theory questions that give a good representation of the theory covered in the course | |