Chapter 2
Pressure Distribution in a Fluid
Pressure Distribution in a Fluid
Overview
The second chapter deals with fluid statics, i.e., the pressure distribution and forces related to pressure in a fluid at rest. Buoyancy and cavitation are also discussed.
So what is pressure?
- Pressure is a thermodynamic property
- Pressure is not a force and has no direction
- Forces arise when the molecules of the fluid interacts with the surface of an immersed body
- A force in the surface-normal direction is generated due to the collision of fluid molecules and the surface
Roadmap
Pressure Variation in a Fluid at Rest
The pressure in a static fluid is a point property, independent of orientation
In a fluid at rest there is, by definition, no shear. Analyzing the forces on the arbitrary triangular fluid element depicted below one can see that in a fluid at rest, the pressure changes in the direction of the gravity vector and is proportional to the depth.

Pressure Forces on a Fluid Element

Force balance on an infinitesimal fluid element in a fluid at rest gives
$$dF_x=pdydz-\left(p+\frac{\partial p}{\partial x}dx\right)dydz=-\frac{\partial p}{\partial x}dxdydz$$$$\mathbf{f}_p=-\nabla p$$
where \(\mathbf{f}\) is the net force per unit volume
it is not the pressure but the pressure gradient causing a net force which must be balanced by gravity or acceleration
Equilibrium of a Fluid Element
In general, force balance for a fluid element will include the following forces
- surface forces caused by pressure gradients
- surface forces due to viscous stresses
- body forces (electromagnetic or gravitational potentials)
Newton's second law:
$$\sum \mathbf{f}=\mathbf{f}_p+\mathbf{f}_g+\mathbf{f}_v=-\nabla p+\rho \mathbf{g}+\mathbf{f}_v=\rho\mathbf{a}$$For hydrostatic problems (fluid at rest), there will by definition not be any viscous forces and no acceleration and thus Newtons second law reduces to
$$\nabla p = \rho \mathbf{g}$$\(\nabla p\) is perpendicular everywhere to surfaces of constant \(p\) and thus the normal of constant-pressure surfaces will be aligned with \(\mathbf{g}\)
Hydrostatic Pressure in Liquids
$$\mathbf{g}=-g\mathbf{e}_z$$$$\frac{dp}{dz}=-\rho g$$
$$p_2-p_1=-\int_1^2\rho g dz$$
 $$p_a=p_b=p_c=p_d$$
$$p_A=p_B=p_C\ne p_D$$
$$p_a=p_b=p_c=p_d$$
$$p_A=p_B=p_C\ne p_D$$
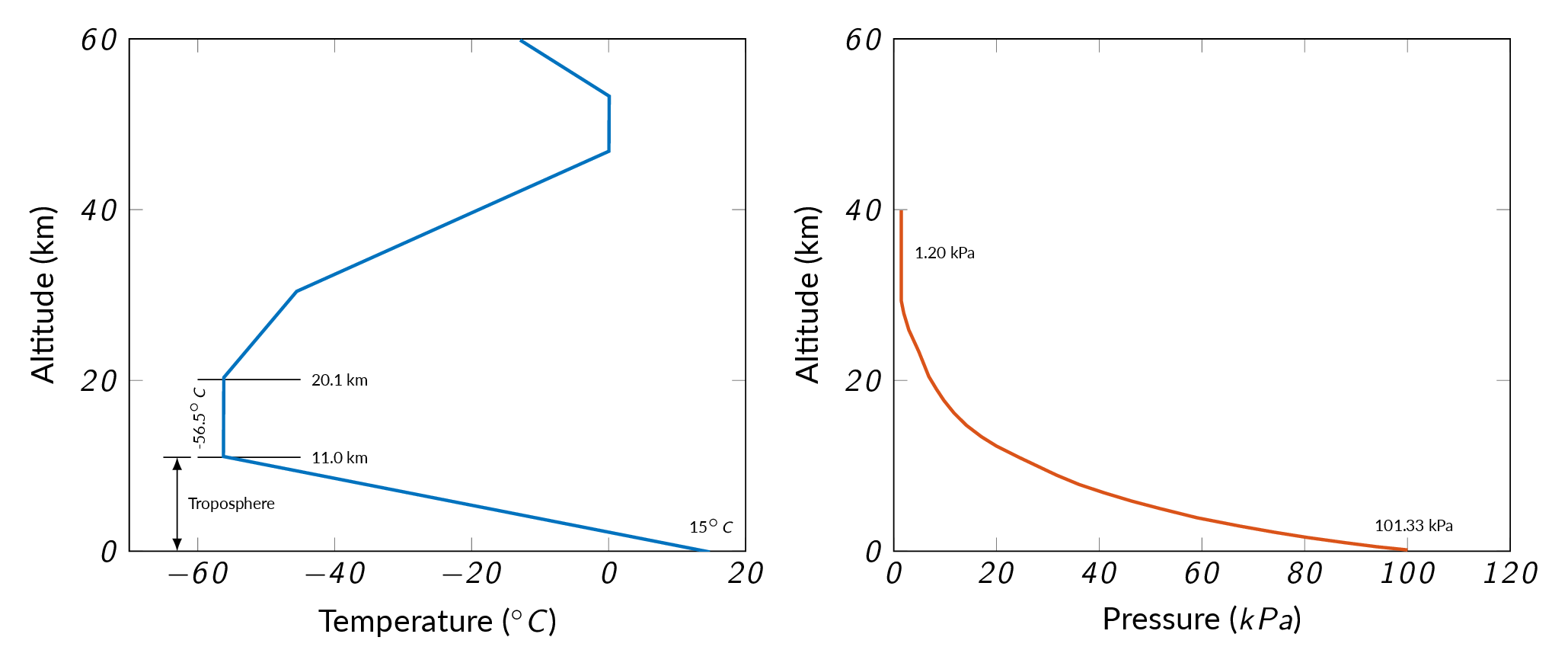
Hydrostatic Pressure in Gases
In a gas the fluid density will vary significantly with pressure and thus density variations must also be considered.
$$\frac{dp}{dz}=-\rho g=-\frac{p}{RT}g$$both pressure and temperature varies with altitude
$$\int_1^2\frac{dp}{p}=\ln \frac{p_2}{p_1}=-\frac{g}{R}\int_1^2\frac{dz}{T}$$
Temperature variation \(T(z)\) needed
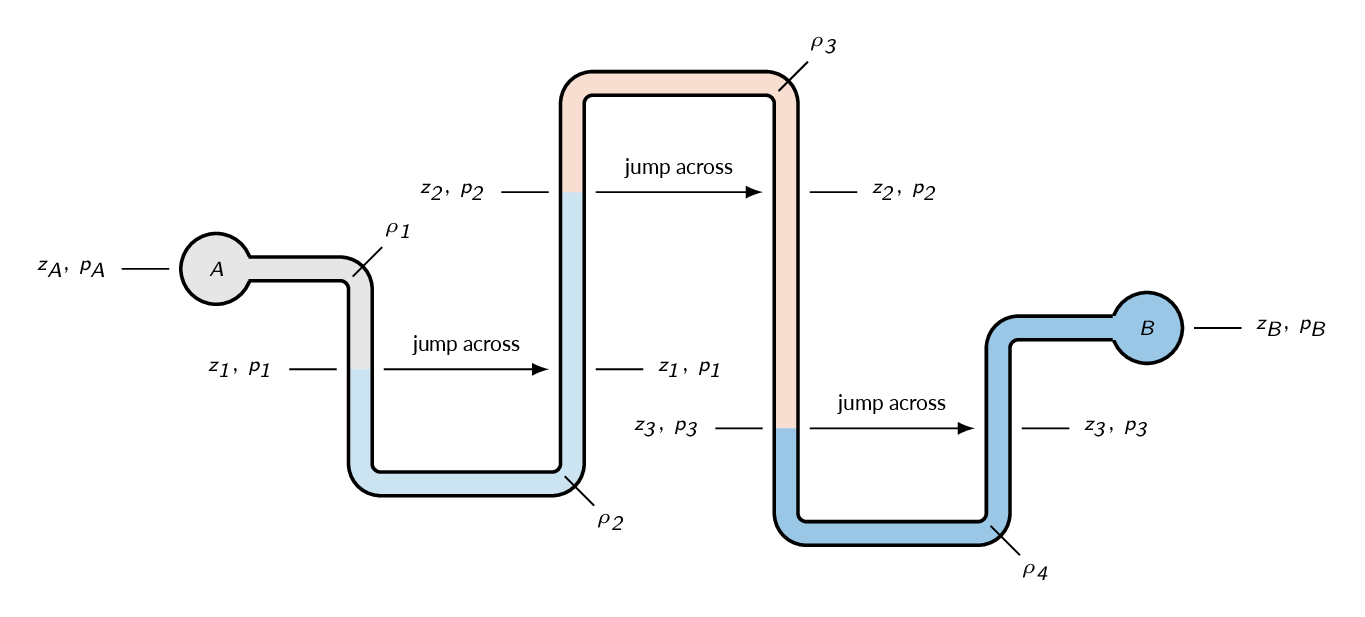
Manometry
Pascal's law:
Any two points at the same elevation in a continuous mass of the same static fluid will be at the same pressure
Buoyancy
Archimedes:$$\mathbf{F}_B=\sum\rho_i g(displacement\ volume)_i$$
A body immersed in a fluid experiences a vertical buoyant force equal to the weight of the fluid it displaces
A floating body displaces its own weight in the fluid in which it floats
For floating bodies
$$\mathbf{F}_B=body\ weight$$
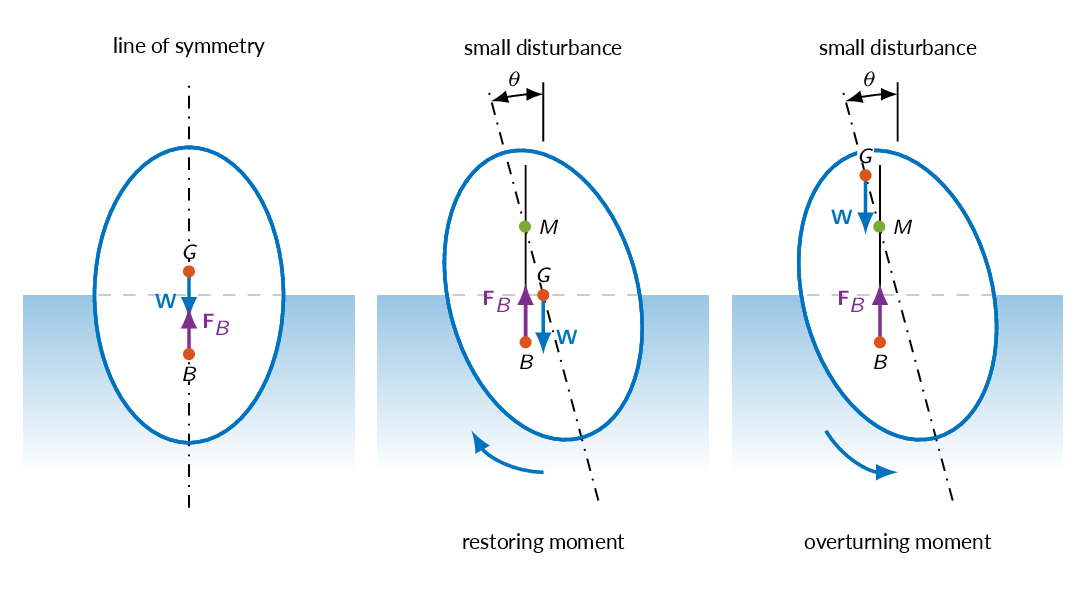
Stability
- \(G\): the center of gravity of a floating body
- \(B\): the center of buoyancy (the center of gravity of the fluid displaced by the body)
- \(M\): meta center (the crossing of a line in the direction of the buoyancy force starting at the center of buoyancy and the symmetry line of the floating body)
If the meta center is above the center of gravity of the floating body it is stable and small disturbances will be restored.
Study Guide
The questions below are intended as a "study guide" and may be helpful when reading the text book.
- If you would hold your thumb tightly over the upper end of straw filled with water and held vertically, would the water not pour out - explain why. Is there a limit for how high a water pillar can be without pouring out? If so, how high can it be?
- Show that the pressure difference in a fluid can be calculated as \(\Delta p=-\rho g\Delta z\) starting from Newton's second law (\(F=ma\)), the fluid density can be assumed to be constant.
- Show that the force balancing gravity in a fluid at rest is caused by the pressure gradient.
- Show that the normal of a constant-pressure surface must be aligned with the gravity vector in a fluid at rest.
- How does the hydrodynamic pressure distribution differ in liquids and gases?
- How can we make use of Pascal's law when analyzing manometer tubes?
- Describe the implication of buoyancy for immersed bodies and floating bodies, respectively.
- How is the buoyancy of a body immersed in a fluid calculated? Show how this relation is obtained.
| Document Archive | ||
| MTF053_C02.pdf | Lecture notes chapter 2 | |
| MTF053_Formulas-Tables-and-Graphs.pdf | A collection of formulas, tables, and graphs | |
| MTF053_Study-Guide.pdf | A collection of theory questions that give a good representation of the theory covered in the course | |